Coins in a circular pattern
Task
Below is a table of diameters of different denominations of United States Coins:
| Denomination | Diameter |
|---|---|
| Dime | $17.9$ mm |
| Nickel | $21.2$ mm |
| Quarter | $24.3$ mm |
| Half Dollar | $30.6$ mm |
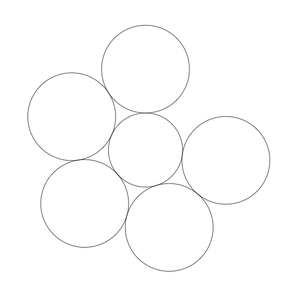
If we place nickels around a central dime, as in the picture below, there is room for five nickels with extra space but not enough room for a sixth nickel:
- How many dimes fit around a central dime? What about around a central nickel, quarter, or half dollar? Do the dimes fit snugly or is there extra space?
- How many half dollars fit around a central dime? What about around a central nickel, quarter, or half dollar? Do the half dollars fit snugly or is there extra room?
- Extending the work in (a) and (b) above, for positive numbers $r$ and $s$ how many circles of radius $s$ will fit around a central circle of radius $r$?
IM Commentary
This task complements ''Seven Circles'' I, II, and III. This is a hands-on activity which students could work on at many different levels and the activity leads to many interesting questions for further investigation:
- Students should find that $6$ pennies fit around a central penny and $6$ half dollars fit around a central half dollar: and the fit should be snug in both cases. This is related to the fact that all circles of the same size are congruent.
- Once the size of a central circle is chosen, the smaller the radius of the surrounding circles, the more of these smaller circles will fit around the middle one. The relationship, however, is extremely complicated: it is not linear, or quadratic, or exponential. The problem ''Seven Circles III'' investigates this relationship which is ''trigonometric'' in nature.
- The diameters for the different denominations are not exact: they have been taken from ''A guidebook of United States Coins.'' Rather than giving the table to students, they could be prompted to measure the diameters and then care is needed to determine how to report these measurements and their level of accuracy.
- One very interesting open ended question would be how to choose sizes of coins to get a snug fit, other than seven coins of the same size.
This task is intended for instructional purposes as an interesting activity which could accompany the other ''Seven Circles'' tasks. If it precedes these tasks, then the focus should be on recording information and looking for patterns. If it is done after these tasks, then students should be prompted to try predict the answers to (a) and (b) before checking experimentally: the work of ''Seven Circles III'' shows that in order to fit $k$ circles of radius $s$ around a central circle of radius $r$, with no space in between, we need $$ \sin{\left(\frac{360}{2k}\right)} = \frac{s}{r+s}. $$ The second solution develops this line of reasoning in full.
Solutions
Solution: 1. Experimentation
- Around a central dime, $6$ dimes fit with no extra space. Around a central nickel, $6$ dimes still fit but with extra space. Around a central quarter, $7$ dimes fit with extra space. Around a central half dollar, $8$ dimes fit with extra room.
- Around a central dime, $4$ half dollars fit with some extra space. Around a central nickel, $4$ half dollars fit with a lot of extra space, almost enough space for a fifth half dollar: the fifth half dollar is so close to fitting that it may not be possible to tell with physical coins whether or not it does fit. Around a central quarter, $5$ half dollars fit with extra space. Around a central half dollar, $6$ half dollars fit with no extra space.
- The number of circles of radius $s$ which can be fit around a central circle of radius $r$ depends only on the fraction $r/s$. This is because all of the circles can be scaled in size and this will not impact the fraction $r/s$ or the number of circles of radius $s$ which fit around the circle of radius $r$. To fit more circles, we need a larger value for $r/s$. The exact depdence, however, is not simple and is calculated in the second solution below.
Solution: 2. Calculation with Trigonometry
-
We begin by reviewing the argument from ''Seven Circles'' III to derive a general formula for how many circles of radius $s$ will fit around a circle of radius $r$. Suppose $C_1$ and $C_2$ are circles of radius $s$ which each touch a circle of radius $r$ and also touch one another as shown in the picture below:

Triangle $POQ$ is an isosceles triangle since $|OP| = |OQ| = r + s$. If $R$ is the midpoint of segment $PQ$ then triangles $OPR$ and $OQR$ are similar by $SSS$. We also have $$ \sin{\angle ROP} = \frac{s}{r+s} $$ since the side opposite angle $ROP$ is $RP$ and the hypotenuse of the right triangle is $OP$. In order for $k$ circles of radius $s$ to fit around a central circle of radius $r$ we will need, writing $m(\angle ROP)$ for the measure of angle $ROP$ in degrees, $$ m(\angle ROP) \leq \frac{360}{2k}: $$ note that the $2k$ in the denominator comes from observing that if $k$ circles fit exactly in the outer ring then this divides the $360$ degrees of the cirlce into $2k$ angles each congruent to angle $ROP$. Rearranging this expression, we find that $$ 2k \leq \frac{360}{m(\angle (ROP))}. $$ In other words, the largest number $k$ of circles of radius $s$ that fit around a circle of radius $r$ is the largest whole number less than or equal to $\frac{360}{2m(\angle (ROP))}$.
We now use this to calculate how many dimes will fit around a central dime, nickel, quarter, and half dollar. If the central coin is a dime then $r = s = \frac{17.9}{2}$ mm. So here we have $\frac{s}{r+s} = \frac{1}{2}$. We have $\sin {30} = \frac{1}{2}$ and so to fit $k$ dimes around a central dime we require $$ 2k \leq \frac{360}{30} = 12 $$ or $k \leq 6$. Moreover, when $k = 6$ we have equality which means that the six dimes fit exactly. Another way to see this is the following: since $m(\angle (ROP)) = 30$ angle $POQ$ is a $60$ degree angle and this means that there will be room for exactly $6$ dimes which will occupy all $360$ degrees of the central circle. With a nickel, quarter, or half dollar in the center, the same method applies and we put the relevant calculations in a table:
Central Coin $\frac{s}{r+s}$ $m(\angle (ROP))$ How many dimes? Nickel 0.458 27.3 6 Quarter 0.424 25.1 7 Half Dollar 0.369 21.7 8 -
We repeat the calculation at the end of part (a), changing the central coin which changes the value of $r$: since the central coin is now a half dollar, the value of $r$ is $\frac{30.6}{2}$ mm instead of $\frac{17.9}{2}$ mm as in part (a).
Central Coin $\frac{s}{r+s}$ $m(\angle (ROP))$ How many half dollars? Dime 0.631 39.1 4 Nickel 0.591 36.2 4 Quarter 0.557 33.8 5 Half Dollar 0.5 30 6 One interesting thing to note from this table is that when placing half dollars around a nickel, it is extremely close to being possible to fit a fifth half dollar, so close that it might not be possible to tell with actual coins whether or not the fifth one fits!
- The method used in parts (a) and (b) allows us to determine in general how many circles of radius $s$ will fit around a central circle of radius $r$. In order to fit $k$ circles of radius $s$ around a circle of radius $r$ we need $$ 2k m(\angle ROP) \leq 360. $$ So this means that $m(\angle ROP) \leq \frac{360}{2k}$. We are given $$ \sin{ROP} = \frac{s}{r+s} $$ and this allows, with a calculator to find $m(\angle ROP)$ and then we can find the largest positive integer $k$ so that $m(\angle ROP)\leq \frac{360}{2k}$. This will be the largest number of circles of radius $s$ which fit around a central circle of radius $r$.
Coins in a circular pattern
Below is a table of diameters of different denominations of United States Coins:
| Denomination | Diameter |
|---|---|
| Dime | $17.9$ mm |
| Nickel | $21.2$ mm |
| Quarter | $24.3$ mm |
| Half Dollar | $30.6$ mm |
If we place nickels around a central dime, as in the picture below, there is room for five nickels with extra space but not enough room for a sixth nickel:

- How many dimes fit around a central dime? What about around a central nickel, quarter, or half dollar? Do the dimes fit snugly or is there extra space?
- How many half dollars fit around a central dime? What about around a central nickel, quarter, or half dollar? Do the half dollars fit snugly or is there extra room?
- Extending the work in (a) and (b) above, for positive numbers $r$ and $s$ how many circles of radius $s$ will fit around a central circle of radius $r$?
