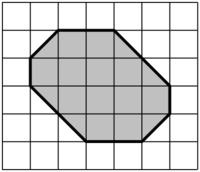
Finding Areas of Polygons
Task
Find the area that is shaded in each figure in at least two different ways.
IM Commentary
This task asks students to find the area of polygons that are best suited for increasingly abstract methods:
- Part (a) of this task asks students to find the area of a polygon that can be found by simply counting the whole number of square units, although there is an advantage to subdividing it into rectangles.
- The area of the figure in part (b) can be found by subdividing it into two right triangles and recombining them into a rectangle.
- The area of the figure in part (c) can be found by subdividing it and recombining the pieces into rectangles, but there is some advantage to seeing the area as what is left over after subtracting the area of some simple triangles from an enclosing rectangle.
- Part (d) is most easily found by enclosing the triangle in a rectangle and subtracting the areas of three right triangles.
Solution
-
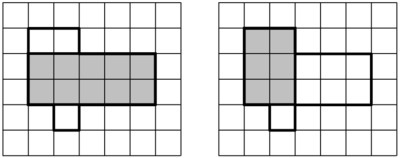
On the left we can see that the figure is composed of a rectangle with area of $2\cdot5=10$ square units plus another with area 2 and a third with area 1 square unit. So the total area is $$10+2+1 = 13 \text{ square units.}$$ On the right we can see that the area is composed of two rectangles and a single square: $$2(2\cdot3)+1 = 13.$$ In either case, we see the area is 13 square units.
-
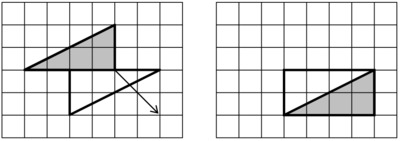
In the figure above, we see that we can subdivide the figure into two right triangles that can be recombined into a rectangle with length 4 units and width 2 units. So the area is $4\cdot 2 = 8$ square units.

Another way to look at this figure is to cut off the small triangles that "stick out" on the sides and place them so they complete a rectangle that has a length of 2 units and a width of 4 units. So the area of the figure is equivalent to a rectangle with area $2\cdot4=8$ square units.
-

This figure shows that if we are persistent, we can decompose this figure into a bunch of triangles with area $\frac12$ square unit along with some rectangles. Moving them around and adding everything up, we see the area is 15 square units.
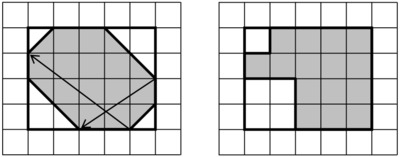
We can find the area in fewer steps if we "enclose" the figure with a rectangle. Now we can see that we can recombine the "white space" into a square with area 1 square unit and another with area 4 square units. The entire rectangle has area $4\cdot5$ square units, so the area of the original figure is $$20-4-1=15 \text{ square units.}$$
-
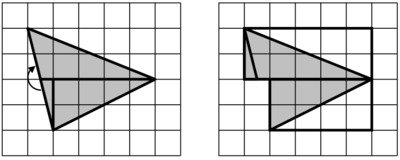
There is a clever way to do it by moving pieces around that shows the area of the figure is the sum of the area of two right triangles, one of which has an area that is half a 2 by 5 rectangle and the other of which is a 2 by 4 rectangle. All told, this means the area of the original triangle is $5+4 = 9$ square units.

This is the figure where it is most helpful to understand that since the area of non-overlapping regions is additive, it can also be subtracted. If the triangle is "enclosed" by a rectangle with area $4\cdot5=20$ square units, we can subtract the area of three right triangles, each with area 2, 4, and 5. So the area of the original triangle is $20-2-4-5=9$ square units, as we found before.
Finding Areas of Polygons
Find the area that is shaded in each figure in at least two different ways.