2 Units Wide and 3 Units Long
Task
Here is a rectangle that is 2 units wide and 3 units long and has an area of 6 square units.

If the unit length is one-tenth, then this rectangle could represent the equation $0.2Â \times 0.3Â = ?$.
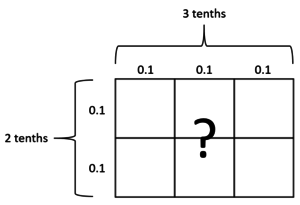
The two-by-three rectangle can also represent the following multiplication equations. For each one, draw a new rectangle and label the side lengths so it represents the multiplication equation. What is the area of a single square in the new rectangle? What is the product of the equation?
- $2,000\times3,000=?$
- $20\times30=?$
- $0.02\times0.03=?$
- $0.0002\times0.0003=?$
IM Commentary
The purpose of this task is for students to notice how the decimal point behaves when numbers in the same place (both in the hundreds, both in the thousandths, etc) are multiplied, and might be followed by the task 12 Rectangular Units. It leverages students' understanding from grade 5 about patterns in the number of zeros of a product when multiplying by powers of 10 and patterns in the placement of a decimal point when a decimal is multiplied by a power of 10 (5.NBT.A.2). Parts (a) and (b) are problems students should already be able to do as a result of their work in 5.NBT.B.7. With this task, we make sure that work is attached to a visual to set students up to understand multiplying any number of decimals.Â
Students can quickly generate the two-by-three grid diagrams if they are provided with blank graph paper. It might help for the teacher to quickly demonstrate creating a grid to draw on and thinking out loud about the sample product $0.2\times0.3$.Â
In follow-up discussion, the teacher should make sure everyone notices how parts (c) and (d) work out, for example:

Students may harbor some misconceptions or just poorly-understood procedures before beginning work on this task, especially related to the number of zeroes instead of the number of places to the left or right of the decimal point. For example, a student may get $0.02 \times 0.03 = 0.0006$ correct because the number of zeroes stays the same (four on the left and four on the right). This strategy will break down with a problem like $0.02 \times 0.05 = 0.001$, so it's important to be on the lookout for incorrect strategies like these. This particular strategy could be thwarted by noting that $.02 \times .03 = .0006$ means the same thing. To promote understanding, we suggest two approaches. First, route each problem back to the area of rectangles. In the diagram of $0.02 \times 0.03$, you can see that the area, which is the same value as this product, consists of six squares each with an area of $0.0006$. Secondly, this reasoning could be written down explicitly using the associative and commutative properties of multiplication:
$$0.02\times0.03$$
$$(2\times0.01)\times(3\times0.01)$$
$$(2\times3)\times(0.01\times0.01)$$
$$6\times0.0001$$
$$0.0006$$
Solution
- $2,000\times3,000$

The area of a single square is $1,000\times1,000=1,000,000$. The product is $6,000,000$. - $20\times30$

The area of a single square is $10\times10=100$. The product is $600$. - $0.02\times0.03$

The area of a single square is $0.01\times0.01=0.0001$. The product is $0.0006$. - $0.0002\times0.0003$

The area of a single square is $0.0001\times0.0001=0.00000001$. The product is $0.00000006$.
2 Units Wide and 3 Units Long
Here is a rectangle that is 2 units wide and 3 units long and has an area of 6 square units.

If the unit length is one-tenth, then this rectangle could represent the equation $0.2Â \times 0.3Â = ?$.

The two-by-three rectangle can also represent the following multiplication equations. For each one, draw a new rectangle and label the side lengths so it represents the multiplication equation. What is the area of a single square in the new rectangle? What is the product of the equation?
- $2,000\times3,000=?$
- $20\times30=?$
- $0.02\times0.03=?$
- $0.0002\times0.0003=?$
