Dividing by a Fraction is the Same as Multiplying by its Reciprocal
Task
Part 1: Match each of the three equations with one of the two diagrams below. Explain how the diagram represents the equation.
$$\frac{2}{3}\times 5 = ?$$
$$\frac{2}{3}\times ? = 5$$
$$\frac{3}{2}\times 5 = ?$$

Part 2: Explain how the diagram below represents both of the equations below.
$$\frac{3}{5}\times ? = A$$
$$\frac{5}{3}\times AÂ = ?$$
Write the first equation as a division equation. Put it together with the second equation without a ? in it.
IM Commentary
The purpose of this task is to help students understand that when we divide by a fraction, it is the same as multiplying by its reciprocal. By carrying out this work outside of a context, students can focus on numbers and operations. This task builds on the work of 5.NF.B, where students represented many different fractional multiplication and division contexts with diagrams.
Some students may approach this task with a trick learned previously like "Keep Change Flip" (or your local variant). Teachers may have to push student thinking when they reach for tricks like this one. In this task, a teacher might stress that the unknown values are not that interesting, and the task doesn't ask us to find them. The goal of the task is for students to understand and be able to explain how the diagrams relate to the equations.Â
Students will likely need some help extracting the mathematical import of the last question, so a whole-class discussion after students have worked on this task either individually or in groups would be appropriate. After understanding, justifying, and later practicing the "invert and multiply" algorithm, students can start to move away from drawing diagrams in order to solve fraction division problems.
Algebraic arguments for understanding this rule are also available after students have done work with equations of the form $px = q$ (6.EE.B.7). Here is a sequence of problems in this vein:
- We can solve the equation $2x = 7$ by either dividing both sides by 2 or multiplying both sides of the equation by $\frac12$.
- We can solve the equation $\frac13x = 7$ by either dividing both sides by $\frac13$ or multiplying both sides by 3.
-  We can solve the equation $\frac45x = 7$ by either dividing both sides by $\frac45$ or multiplying both sides by $\frac54$.
The goal is for students to understand and remember the invert and multiply rule, but at some point they should be able to use it without revisiting these reasons every time.Â
Solution
Part 1:

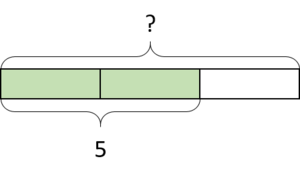
The blue part of the rectangle (which is ?) represents $\frac23$ of the rectangle because the entire rectangle is partitioned into 3 equal pieces and 2 are shaded. Since the entire rectangle is 5, the blue part is $\frac23$ of 5, so this diagram represents $\frac{2}{3}\times 5 = ?$.
Â

The green part of the rectangle (which is 5) represents $\frac23$ of the rectangle because the entire rectangle is partitioned into 3 equal pieces and 2 are shaded. Since the entire rectangle is ?, the green part is $\frac23$ of ?, so this diagram represents $\frac{2}{3}\times ? = 5$.
This diagram also represents $\frac{3}{2}\times 5 = ?$ because you can look at each piece as half of the green part (which is 5), and since there are three pieces, the entire rectangle is $\frac32$ of 5.
Â
Part 2:

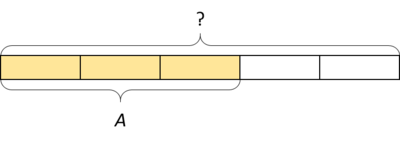
The yellow part (which represents $A$) is 3 of 5 equal parts of the entire rectangle (whish represents the unknown ?), so AÂ is $\frac35$ of ?. This is the same as $\frac35 \times ? = A$. This equation can be re-written as $A \div \frac35 = ?$ because of the relationship between multiplication and division.
We can also see the entire rectangle as $\frac53$ of the yellow part, since the yellow part is divided into 3 equal pieces and the entire rectangle is 5 of those pieces. So the diagram also represents $\frac53 \times A = ?$.
If we put these two equations together:
$$A \div \frac35 = ?$$
$$\frac53 \times A = ?$$
we getÂ
$A \div \frac35 =Â \frac53 \times A = A \times \frac53$ orÂ
$$A \div \frac35 = A \times \frac53$$Â
Dividing by a Fraction is the Same as Multiplying by its Reciprocal
Part 1: Match each of the three equations with one of the two diagrams below. Explain how the diagram represents the equation.
$$\frac{2}{3}\times 5 = ?$$
$$\frac{2}{3}\times ? = 5$$
$$\frac{3}{2}\times 5 = ?$$


Part 2: Explain how the diagram below represents both of the equations below.

$$\frac{3}{5}\times ? = A$$
$$\frac{5}{3}\times AÂ = ?$$
Write the first equation as a division equation. Put it together with the second equation without a ? in it.
