Constructing Special Angles
Task
The goal of this task is to estimate the measure of angles in triangles with integer side lengths.
- What are the angle measures in a triangle whose three sides each have length of one unit? Â Explain.
- What are the approximate measures of the three angles in a triangle whose side lengths are 3, 4, and 5 units respectively? Explain.
- What are the approximate angle measures of the three angles in a triangle whose side lengths are 2, 3, and 4 units respectively?
IM Commentary
The goal of this task is to estimate the measure of angles in triangles with integer side lengths. In some cases, like the equilateral triangle, this can be done using properties of the triangle. For right triangles, inverse trigonometric functions can be applied. In other cases, like part (c), an auxiliary construction is needed before applying trigonometry to calculate the angles. Since the task requires inverse trigonometric functions, students will use technology to make appropriate estimates. One very interesting side note to this task is that the algorithms that many calculators use in order to calculate complex functions such as trigonometric functions use properties of trigonometric functions along with some exact values for special angles like 30$^\circ$ and 45$^\circ$. Â
Many ancient cultures reportedly used triangles with side lengths 3, 4, and 5 units in order to construct right angles. This provided a simple means of making right angles which would be very important in architecture and other design problems. More information about how ancient cultures used Pythagorean triples in order to construct right angles can be found in the commentary to this task: https://www.illustrativemathematics.org/illustrations/724. One very interesting and challenging extension question would be: what whole number side lengths are necessary in order to construct angles within one half of a degree of each whole number angle measure from 0 to 179? Or we could look for angles within any given level of precision (one degree or one tenth of a degree, for example) of any given angle.Â
Solution
- A triangle with three sides of length 1 unit is an equilateral triangle, and so all of its angles are congruent and each measures 60 degrees.
- The converse of the Pythagorean theorem says that if $a, b, c$ are side lengths of a triangle and $a^2 + b^2 = c^2$ then the triangle is right with the right angle opposite the side of length $c$. In our case, this is pictured below:
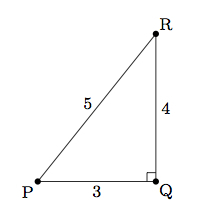
We know that for the angle $P$ the side adjacent measures 3 units, the side opposite measures 4 units, and the hypotenuse of the right triangle measures 5 units. So $\sin{P} = \frac{4}{5}$ and $\cos{P} = \frac{3}{5}$. So we have $m(P) = \sin^{-1}{\left(\frac{4}{5}\right)} \approx 53^\circ$. Since $m(\angle P) + m(\angle R) = 90$ we have that $m(\angle R) \approx 37^\circ$ which can also be found using $m(\angle R) = \sin^{-1}{\left(\frac{3}{5}\right)}$. Â
-
Below is a picture of a triangle with side lengths 2, 3, and 4 units along with a perpendicular line drawn to the side of length 4:

In order to estimate the different angles we begin by calculating the segment lengths $|AD|$, $|BD|$, and  $|CD|$. We can do this by applying the Pythagorean theorem to right triangles $ADC$ and $BDC$. We set $x = |CD|$ and $y = |DB|$ so $|AD| = 4 - y$. The Pythagorean theorem applied to $\triangle BDC$ gives $$x^2 + y^2 = 4.$$ Applying the Pythagorean theorem to $\triangle ADC$ gives $$x^2 + (4-y)^2 = 9.$$ We can eliminate $x$ from the equations by subtracting the first from the second, leaving us with $(4-y)^2 - y^2 = 5$. This is a linear equation in $y$ which we can solve to find $y = \frac{11}{8}$. This tells us that $|BD| = \frac{11}{8}$ and so $|AD| = \frac{21}{8}$. Using either of the above equations we find that $|CD| = \frac{\sqrt{135}}{8}$.
We can now estimate the different angles. We have $\sin{A} = \frac{\sqrt{135}}{24}$ so $m(A) = \sin^{-1}\left(\frac{\sqrt{135}}{24}\right) \approx 29^\circ.$ For angle $B$ we have $\sin{B} = \frac{\sqrt{135}}{24}$ so $m(B) = \sin^{-1}\left(\frac{\sqrt{135}}{16}\right) \approx 47^\circ.$ For $\angle ACB$ we can use the fact that the sum of the three angles in $\triangle ABC$ is 180$^\circ$ to get an estimate of 104$^\circ$.Â
Constructing Special Angles
The goal of this task is to estimate the measure of angles in triangles with integer side lengths.
- What are the angle measures in a triangle whose three sides each have length of one unit? Â Explain.
- What are the approximate measures of the three angles in a triangle whose side lengths are 3, 4, and 5 units respectively? Explain.
- What are the approximate angle measures of the three angles in a triangle whose side lengths are 2, 3, and 4 units respectively?
