Sum of angles in a polygon
Task
-
Below is a quadrilateral $ABCD$:

Show, by dividing $ABCD$ into triangles, that the sum of the interior angles is $360^\circ$: $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) = 360. $$
-
Below is a pentagon $ABCDE$:

Show that the sum of the interior angles is $540^\circ$: $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) + m(\angle E) = 540. $$
- Suppose $P$ is a polygon with $n \geq 3$ sides and assume that all interior angles of $P$ measure less than $180$ degrees. Show that the sum of the measures of the interior angles of $P$ is $$ (n-2) \times 180 \,\,\mbox{degrees}. $$ Check that this formula gives the correct value for equilateral triangles and squares.
IM Commentary
This problem provides students with an opportunity to discover algebraic structure in a geometric context. More specifically, the student will need to divide up the given polygons into triangles and then use the fact that the sum of the angles in each triangle is $180^\circ$. The algebraic formula which occurs in step (c) can be seen as a generalization of parts (a) and (b) but an argument establishing this formula requires a delicate argument which successively reduces the number of sides of the polygon in question. Alternatively, step (c) can be accomplished by providing an explicit division of the given polygon into triangles. Both solutions are provided and it is important to note that the logic is rather different: for the first solution, the case of a polygon with $n$ sides is reduced to the case of a polygon with one fewer, or $n-1$ sides. This argument requires subscripts and the teacher may wish to provide guidance here. The second argument is a direct generalization, a careful subdivision into triangles for parts (a) and (b) and requires much less work with subscripts.
When the polygon has angles measuring more than $180$ degrees the result is still true but more care is needed to explain why. For example, in the picture below the quadrilateral has one reflex angle (that is, one angle measuring greater than 180 degrees):
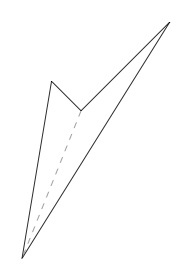
The sum of the four angles is still equal to $360$ degrees, however, as can be seen by drawing the auxiliary line indicated which divides the quadrilateral into two triangles. The division needs to be done carefully, however, if there are several angles measuring over $180$ degrees which may occur for polygons with more sides. This could make for a challenging and interesting classroom activity. The pentagon in part (b) was chosen with one angle measuring greater than $180$ degrees in order to give students a chance to think about how to deal with this situation.
This task illustrates three of the mathematical practices. The first two parts require a careful combination of geometric and algebraic reasoning (MP2) and, in order to provide a convincing argument (MP3), the algebra and geometry need to be carefully linked. This link is accomplished through a picture which the students must provide. Finally, in order to complete part (c), students must identify a pattern from parts (a) and (b) and then explain why this works for a polygon with any number of sides: this is a good example of MP8.
Solutions
Solution: 1
-
We can divide the quadrilateral $ABCD$ into two triangles by drawing segment $\overline{AC}$ as below:

The sum of the angles in triangle $ABC$ is $180$ degrees and the sum of the angles in triangle $ACD$ is $180$ degrees:
\begin{align} m(\angle CAB) + m(\angle B) + m(\angle BCA) &= 180 \\ m(\angle CAD) + m(\angle D) + m(\angle DCA) &= 180. \end{align}We have $m(\angle CAB) + m(\angle CAD) = m(\angle A)$ and $m(\angle BCA) + m(\angle DCA) = m(\angle C)$ so adding the above two equations gives $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) = 180 + 180 = 360. $$
The same argument applies if segment $\overline{BD}$ is added instead of segment $\overline{AC}$.
-
As in part (a) we divide the pentagon into triangles by connecting some of its vertices. We have to be careful here to make sure that the segments joining vertices do not go outside of the pentagon and we also do not want these segments to cross inside of the pentagon:

We have divided pentagon $ABCDE$ into triangles $ABC$, $CDE$, and $ACE$. The sum of the angles in each of these triangles is 180 degrees:
\begin{align} m(\angle CAB) + m(\angle B) + m(\angle BCA) &= 180 \\ m(\angle ECD) + m(\angle D) + m(\angle DEC) &= 180\\ m(\angle EAC) + m(\angle ACE) + m(\angle CEA) &= 180. \end{align}As in part (a) we can use the facts that $m(\angle BCA) + m(\angle ECD) + m(\angle ACE) = m(\angle C)$, $m(\angle DEC) + m(\angle CEA) = m(\angle E)$, and $m(\angle CAB) + m(\angle EAC) = m(\angle A)$ to conclude, adding these three equations, that $$ m(\angle A) + m (\angle B) + m(\angle C) + m(\angle D) + m(\angle E) = 540. $$
There is a second way to show that the sum of the angles in pentagon $ABCDE$ is $540$ degrees which helps build an intuition for part (c) below. We know from part (a) that the sum of the angles in quadrilateral $ABCE$ is $360$ degrees: $$ m(\angle A) + m(\angle B) + m(\angle BCE) + m(\angle AEC) = 360. $$ We also know that the sum of the angles in triangle $CDE$ is $180$ degrees: $$ m(\angle D) + m(\angle CED) + m(\angle ECD) = 180. $$ Since $m(\angle BCE) + m(\angle ECD) = m(\angle C)$ and $m(\angle AEC) + m(\angle CED) = m(\angle E)$ we can add these two equations to conclude again that $$ m(\angle A) + m (\angle B) + m(\angle C) + m(\angle D) + m(\angle E) = 540. $$
-
We may assume that the polygon in question has at least $n \geq 6$ sides because quadrilaterals and pentagons have been treated in parts (a) and (b) above. We will call the original polygon with $n$ sides $P_n$. We begin by identifying three successive vertices $A,B,C$ on the polygon and drawing segment $AC$ as pictured below:

Since none of the angles in the polygon are greater than $180$ degrees, segment $\overline{AC}$ divides the polygon into triangle $ABC$ and a new polygon with $n - 1$ sides which omits vertex $B$. We call this new polygon $P_{n-1}$. The sum of the angles of $P_n$ is the sum of the angles of $P_{n-1}$ together with the angles of triangle $ABC$: $$ \mbox{Sum of angles of $P_n$} = 180 + \mbox{Sum of angles of $P_{n-1}$.} $$
We can now apply the same argument to $P_{n-1}$, dividing it into a triangle and a polygon with $n-2$ sides which we call $P_{n-2}$: $$ \mbox{Sum of angles of $P_{n-1}$} = 180 + \mbox{Sum of angles of $P_{n-2}$.} $$ Combining these two formulas gives $$ \mbox{Sum of angles of $P_n$} = 360 + \mbox{Sum of angles of $P_{n-2}$.} $$ We can continue this process until we reach a triangle, $P_3$, and we will find $$ \mbox{Sum of angles of $P_n$} = (n-3) \times 180 + \mbox{Sum of angles of $P_{n-(n-3)}$.} $$ The sum of the angles of the triangle $P_3 = P_{n-(n-3)}$ is $180$ so we find $$ \mbox{Sum of angles of $P_n$} = (n-2) \times 180 \,\,\mbox{degrees.} $$
Plugging in $n = 4$ and $n = 5$ to the formula gives $360^\circ$ for the sum of the angles of a quadrilateral and $540^\circ$ for the sum of the angles of a pentagon.
Solution: 2. Alternate approach
-
Instead of dividing quadrilateral $ABCD$ into two triangles, another method uses an interior point of the quadrilateral to make four triangles as pictured below:

Since the sum of the angles in a triangle is $180^\circ$ we have
\begin{align} m(\angle OAB) + m(\angle OBA) + m(\angle AOB) &= 180 \\ m(\angle OBC) + m(\angle OCB) + m(\angle BOC) &= 180\\ m(\angle OCD) + m(\angle ODC) + m(\angle COD) &= 180\\ m(\angle ODA) + m(\angle OAD) + m(\angle DOA) &= 180. \end{align}So adding all twelve of these angles gives $4 \times 180^\circ = 720^\circ$. We know that
\begin{align} m(\angle OAB) + m(\angle OAD) &= m(\angle A) \\ m(\angle OBC) + m(\angle OBA) &= m(\angle B)\\ m(\angle OCD) + m(\angle OCB) &= m(\angle C)\\ m(\angle ODA) + m(\angle ODC) &= m(\angle D). \end{align}This leaves the four angles which are interior to the quadrilateral: $\angle AOB$, $\angle BOC$, $\angle COD$, and $\angle DOA$. These four angles make a full circle which means that $$ m(\angle AOB) + m(\angle BOC) + m(\angle COD) + m(\angle DOA) = 360. $$ Putting all of this information together we conclude that $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) =720 - 360 = 360. $$
-
The same method applies to the pentagon $ABCDE$ provided we carefully choose an interior point, as below:

Since the sum of the angles in a triangle is $180^\circ$ we have
\begin{align} m(\angle OAB) + m(\angle OBA) + m(\angle AOB) &= 180 \\ m(\angle OBC) + m(\angle OCB) + m(\angle BOC) &= 180\\ m(\angle OCD) + m(\angle ODC) + m(\angle COD) &= 180\\ m(\angle ODE) + m(\angle OED) + m(\angle EOD) &= 180\\ m(\angle OEA) + m(\angle OAE) + m(\angle EOA) &= 180. \end{align}So adding all fifteen of these angles gives $5 \times 180^\circ = 900^\circ$. We know that
\begin{align} m(\angle OAB) + m(\angle OAE) &= m(\angle A) \\ m(\angle OBC) + m(\angle OBA) &= m(\angle B)\\ m(\angle OCD) + m(\angle OCB) &= m(\angle C)\\ m(\angle ODE) + m(\angle ODC) &= m(\angle D)\\ m(\angle OEA) + m(\angle OED) &= m(\angle E). \end{align}This leaves the five angles which are interior to the quadrilateral: $\angle AOB$, $\angle BOC$, $\angle COD$, $\angle DOE$, and $\angle EOA$. These five angles make a full circle which means that $$ m(\angle AOB) + m(\angle BOC) + m(\angle COD) + m(\angle DOE) + m(\angle EOA) = 360. $$ Putting all of this information together we conclude that $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) + m(\angle E) = 900 - 360 = 540. $$
-
This method also works for part (c) but we cannot draw a complete picture since we do not know how many sides the polygon $P_n$ has. The assumption that $P_n$ is convex guarantees that any point $O$ on the interior will divide $P_n$ into $n$ triangles by drawing the line segments connecting $O$ to each of the $n$ vertices of $P_n$. The sum of the angles in these $n$ triangles is $n \times 180^\circ$. This gives the sum of the angles of $P_n$ together with the $360^\circ$ of the circle at point $O$. So the sum of the angles of $P_n$ is $(n-2) \times 180^\circ$.
Note that if $P_n$ were not convex then there is no guarantee that there is a point $O$ inside of $P_n$ which can be joined to each vertex of $P_n$ without going outside of the polygon.
Sum of angles in a polygon
-
Below is a quadrilateral $ABCD$:

Show, by dividing $ABCD$ into triangles, that the sum of the interior angles is $360^\circ$: $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) = 360. $$
-
Below is a pentagon $ABCDE$:

Show that the sum of the interior angles is $540^\circ$: $$ m(\angle A) + m(\angle B) + m(\angle C) + m(\angle D) + m(\angle E) = 540. $$
- Suppose $P$ is a polygon with $n \geq 3$ sides and assume that all interior angles of $P$ measure less than $180$ degrees. Show that the sum of the measures of the interior angles of $P$ is $$ (n-2) \times 180 \,\,\mbox{degrees}. $$ Check that this formula gives the correct value for equilateral triangles and squares.
