Introducing the Distributive Property
Task
Part I.
a. How many circles are there in all? Write down a number sentence that shows how you thought about it.

b. Alonso said he figured out how many shaded circles there were first and then how many unshaded circles there were second. Once he knew how many of each, he added them together to find the total. Write a number sentence Alonso could have used that shows his reasoning.
c. Jennifer said, “I just saw 3 rows of 8 circles.” Write a number sentence that Jennifer could have used that shows her reasoning.
Part II.
a. The area model below shows the floor plan for a storage closet. The storage closet will have a tiled floor with grey tiles on the left and white tiles on the right. How many tiles are needed for the storage closet in all? Write down a number sentence that shows how you thought about it.
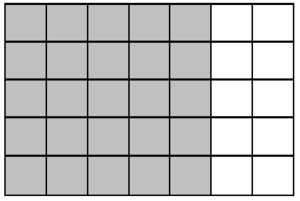
b. Think back to how Alonso figured out how many circles there were in Part I. Use Alonso’s same strategy here to find out how many tiles are needed. Write a number sentence with Alonso’s reasoning.
c. Think back to how Jennifer figured out how many circles there were in Part I. Use Jennifer’s same strategy here to find out how many tiles are needed. Write a number sentence with Jennifer's reasoning.
IM Commentary
This is an instructional task, best used when students are first working with the distributive property. The standard asks students to apply the distributive property to area models, though this task intentionally begins with array models. Students may need to become comfortable with breaking apart discrete sets before breaking apart continuous area models (just as students usually begin understanding multiplication through arrays before transitioning to area models.)
The teacher should facilitate each step of this task. When asking students how many circles they see, push students to think beyond counting. Some students may see 3 rows of 8 while others may see 4 sets of 6! Helping students recognize the equal groups that different students see in the same array is a crucial part of building fluency and flexibility with multiplication.
This task does not explicitly ask students to formally connect Alonso and Jennifer's reasoning strategies as evidence of the distributive property- the teacher will need to make this link explicit after students have had time to think through how Alonso and Jennifer's ways of thinking about the same problem are different. Both ways of thinking yield the same answer.
Solutions
Solution:
Part I

part a.
Solutions may vary. Here are several possibilities:
3 x 8 = 24
4 x 6 = 24 (the six come from every 2 columns of 3 grouped together)
3 x 6 + 3 x 2 = 24
8 + 8 + 8 = 24
part b.
Alonso found that there are 18 shaded dots and 6 unshaded dots, so there are 24 dots in all.
His number sentence would be: 3 x 6 + 3 x 2 = 24
part c.
Jennifer found that there are 24 dots in all.
Her number sentence would be: 3 x 8 = 24
Solution:
Part II

part a.
Solutions may vary. Here are some examples:
5 x 7 = 35
10 + 10 + 10 + 5 = 35
5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
5 x 5 + 10 = 35
part b.
Alonso found 25 shaded tiles and 10 white tiles, so 35 tiles in all.
His number sentence would be: 5 x 5 + 5 x 2 = 35
part c.
Jennifer found 35 tiles in total.
Her number sentence would be: 5 x 7 = 35


