Task
India is remodeling her bathroom. She plans to cover the bathroom floor with tiles that are each 1 square foot. Her bathroom is 5 feet wide and 8 feet long. India needs to stay within a strict budget and must purchase the exact number of tiles needed.
How many tiles should India buy? Use the space below to illustrate your answer.

IM Commentary
This task allows students to use the concept of "tiling" as an entry point to linking area with multiplication. Ideally, they would be given foam or plastic tiles to actually practice putting the tiles on the space without gaps or overlaps.
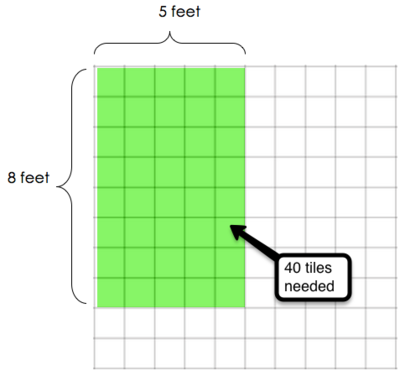
Students may find the total number of tiles needed by counting all, using repeated addition or using multiplication. For the students who do not see the immediate relationship between area and multiplication, it might be helpful to have students explain their reasoning. One student might reason that there are 8 rows of 5 tiles, so there are 8 x 5 or 40 tiles. Another student might reason that there are 5 columns of 8 tiles each, so there are 5 x 8 or 40 tiles.
Teachers will also have to help students understand that they are finding the number of tiles that India needs to remodel the bathroom, but that each tile represents one square foot. We find the number of tiles needed by finding the number of square feet we need to cover.
Solution
India will need to buy 40 tiles because she has 40 square feet of bathroom floor to cover. We can see this as 8 rows with 5 tiles in each row or 5 columns with 8 tiles in each column, so we can find the total number of tiles by multiplying: 8 x 5 = 40. We can illustrate this with a picture as well.