Geometric pictures of one half
Task
For each of the pictures, explain how you can see that half of the square is shaded:
IM Commentary
This task presents students with some creative geometric ways to represent the fraction one half. The goal is both to appeal to students' visual intuition while also providing a hands on activity to decide whether or not two areas are equal. In order for students to be successful with this task, they need to understand that area is additive in the sense described in 3.MD.7d. Students should be given paper models of each picture which they can fold or cut and rearrange so as to help visualize why the shaded and unshaded areas are equal.
Although this task could be used for assessment it is better suited for a classroom activity. After working on these representations of one half, students could be asked to create their own geometric representations of one half of a square and then share these with one another.
The first two pictures introduce them to constructions which will be important as they move forward in studying geometry: the first picture represents a special case that can be generalized to show why the area of a triangle is "one-half of the base times the height," while the second example can be used much later to understand why the diagonal of a square with side length one has length \sqrt{2}.
The Standards for Mathematical Practice focus on the nature of the learning experiences by attending to the thinking processes and habits of mind that students need to develop in order to attain a deep and flexible understanding of mathematics. Certain tasks lend themselves to the demonstration of specific practices by students. The practices that are observable during exploration of a task depend on how instruction unfolds in the classroom. While it is possible that tasks may be connected to several practices, only one practice connection will be discussed in depth. Possible secondary practice connections may be discussed but not in the same degree of detail.
This particular task helps illustrate Mathematical Practice Standard 5, Use appropriate tools strategically. Third graders experience the fraction, one half, by exploring visually and kinesthetically with the ideas of area. Students use paper diagrams of shapes, which they can manipulate to determine if the shaded and unshaded portions each represent one half of the entire picture. As students become proficient in this practice, they will be able to consider the usefulness of this representation and consider its strengths and limitations, as well as know how to use it appropriately. The solution pathway that a student selects needs to make sense to him/her to be able to explain and justify (MP.3). Students will come to realize that certain methods/tools are more efficient and they will abandon less useful tools in favor of more appropriate strategies/tools.
Solutions
Solution: 1
-
Below is a picture of a line where the picture can be cut, or folded, which will help see why the shaded area is one half:

Once the picture is cut, we have two rectangles. For each rectangle, half is shaded and the other half is unshaded. For these rectangles if they are cut along the diagonal where shaded and unshaded parts meet, the two shaded pieces and two unshaded pieces will match up. Therefore the shaded and unshaded areas are equal and so the shaded area represents one half of the square. Alternately, if the picture is folded into two rectangles, the students can observe that the shaded triangles and unshaded triangles have the same size and shape.
-
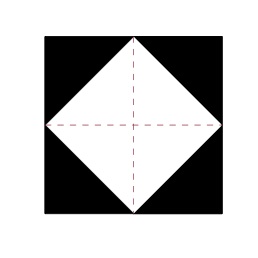
Below are two lines where the picture may be cut or folded to reveal why the shaded area represents one half of the full square:

If two cuts along the indicated lines are made, we have four smaller squares and, just as in part (a), each of these can be cut (or folded) to show that their shaded and unshaded areas are equal. So the total shaded and total unshaded areas here are equal and the shaded area represents one half of the square. As in part (a), the picture can also be folded twice, giving four black and four white triangles all of the same size and shape.
-
For this picture, the circles could be cut out and the white and black circle are the same size. The remaining two black and white pieces also have the same shape and size and so, here too, the shaded and unshaded areas are equal. Alternatively, if a vertical fold is made down the center of the picture, shaded and unshaded areas will match up, showing that each represents one half of the square. This vertical cut line is pictured below:

Solution: Student solution
a. If I split the white triangle along the dotted line, I see 4 triangles that are all the same. Two of the four triangles are shaded, so half the square is shaded.

b. If I split the square along these 2 dotted lines, I see 8 triangles that are all the same. Four of the 8 triangles are shaded, so half the square is shaded.
c. I imagined I cut the shaded circle out, and the white circle out. Since they're the same size, I can swap them to see two rectangles that are the same size. One is shaded, and one isn't, so half the square is shaded.

Geometric pictures of one half
For each of the pictures, explain how you can see that half of the square is shaded:



