All vs. Only some
Alignments to Content Standards:
1.G.A.1
Task
First pose the question:
Here are four triangles. What do all of these triangles have in common? What makes them different from the figures that are not triangles? What is true for some but not all of these triangles?
 If students come up with a statement that is true about all of the triangles that they see but not true of all triangles in general, the teacher should ask students if they can imagine a triangle without that attribute. For example, if a student says, "All of the triangles are white on the inside," the teacher can ask, "Would it be possible for a triangle to have a different color on the inside?" When the class comes up with an attribute that is truly shared by all triangles, then the class can complete the sentence frame: All triangles ___________, but only some triangles _________________. When the students have written (or composed) their sentences based on the sentence frames, the class can write the definition of a triangle together:
If students come up with a statement that is true about all of the triangles that they see but not true of all triangles in general, the teacher should ask students if they can imagine a triangle without that attribute. For example, if a student says, "All of the triangles are white on the inside," the teacher can ask, "Would it be possible for a triangle to have a different color on the inside?" When the class comes up with an attribute that is truly shared by all triangles, then the class can complete the sentence frame: All triangles ___________, but only some triangles _________________. When the students have written (or composed) their sentences based on the sentence frames, the class can write the definition of a triangle together:
A triangle is a closed shape with three straight sides that meet at three corners.
The teacher will repeat the process for rectangles and then squares. Each time, the class should complete the appropriate sentence frame once they have settled on a universal attribute. Then the teacher can help them compose a definition for the shape. 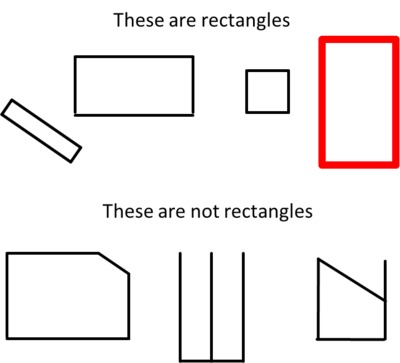
A rectangle is a closed shape with four straight sides and four square corners.
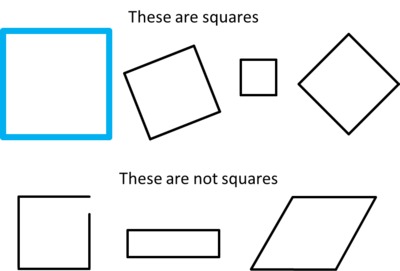
A square is a closed shape with four straight sides and four square corners. The four sides are the same length.
Once the class has working definitions in grade appropriate language for these shapes, students can identify the triangles, rectangles, and squares below. * Color all the triangles blue. * Color all the squares red. * Color all the rectangles green. 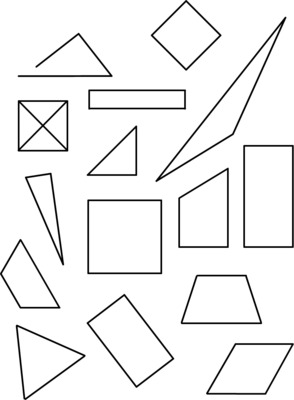
IM Commentary
The purpose of this task is for students to discuss and come to understand what constitute defining attributes for triangles, squares, and rectangles. Students start by looking for attributes shared by all the instances of a particular shape. Some, but not, all of these attributes will be defining attributes. For example, all rectangles have opposite sides parallel, but this isn't a defining attribute--it is something you can show starting only with the defining attributes that a rectangle is a quadrilateral with four right angles. Thus, in the end the teacher will need to state for the students which of those attributes are defining attributes by helping the class write a definition for each shape. Here are some suggestions for modifying or extending this task based on student readiness/needs:
-
The teacher may desire to include an "are" in each sentence so that students only need to fill in single words: All triangles are _____________, but only some triangles are _______________. although this forces students to say (for example) "three-sided" rather than "have three sides".
-
At the end of the lesson the teacher can have students assemble a list of things that are never defining attributes for shapes, such as color, size, and orientation, and things that are often defying attributes for shapes, such as number of sides, number of angles, or if the sides are straight or curved. This will help students to understand what defines shapes in general vs just defining one specific shape.
-
A student may fill in "only some" with something mathematical. While not part of the standard, it may help to also distinguish between non-defining attributes which are not mathematical (such as "drawn in pencil") and ones that have mathematical content that is not relevant to that particular shape (such as "has equal sides").
There is a printable PDF version of the example shapes attached, or the teacher can draw the figures on the board. There is also a printable PDF for the coloring activity.
The Standards for Mathematical Practice focus on the nature of the learning experiences by attending to the thinking processes and habits of mind that students need to develop in order to attain a deep and flexible understanding of mathematics. Certain tasks lend themselves to the demonstration of specific practices by students. The practices that are observable during exploration of a task depend on how instruction unfolds in the classroom. While it is possible that tasks may be connected to several practices, only one practice connection will be discussed in depth. Possible secondary practice connections may be discussed but not in the same degree of detail.
This particular task is linked very intentionally to the first part of Mathematical Practice Standard 3, construct viable arguments. Through question posing, students are guided to distinguish and describe defining characteristics of triangles by examining figures that are triangles and figures that are not triangles. This same process is repeated for squares and rectangles. Thus, students are continually analyzing and describing. This task lays the foundation for the art of explanation leading to “critiquing the reasoning of others.” For instance, a first grader might offer the explanation, “It looks like all the triangles have 3 straight sides that are all connected.” Through carefully crafted questions, students will discover which characteristics really matter and complete the sentence frames provided as a class. These sentence frames can then be used to write definitions for each of the shapes. These types of activities further support MP.6, Attend to precision, which in this case pertains to precision in language.
Solution
Note: Informal language is acceptable, especially in the non-defining attributes. Students do not have to identify all the defining attributes listed below, but the key ones are all included in this solution for completeness.
All triangles have three straight sides, but only some triangles are small.
All triangles have three corners, but only some triangles are green.
All triangles are closed, but only some triangles are upside down.
All rectangles have four straight sides, but only some rectangles are red.
All rectangles have four square corners, but only some rectangles are tall and skinny.
All rectangles are closed, but only some rectangles are short.
All squares have four equal sides, but only some squares are tilted.
All squares have four have four square corners, but only some squares are blue.
All squares are closed, but only some squares are turned.

 If students come up with a statement that is true about all of the triangles that they see but not true of all triangles in general, the teacher should ask students if they can imagine a triangle without that attribute. For example, if a student says, "All of the triangles are white on the inside," the teacher can ask, "Would it be possible for a triangle to have a different color on the inside?" When the class comes up with an attribute that is truly shared by all triangles, then the class can complete the sentence frame: All triangles ___________, but only some triangles _________________. When the students have written (or composed) their sentences based on the sentence frames, the class can write the definition of a triangle together:
If students come up with a statement that is true about all of the triangles that they see but not true of all triangles in general, the teacher should ask students if they can imagine a triangle without that attribute. For example, if a student says, "All of the triangles are white on the inside," the teacher can ask, "Would it be possible for a triangle to have a different color on the inside?" When the class comes up with an attribute that is truly shared by all triangles, then the class can complete the sentence frame: All triangles ___________, but only some triangles _________________. When the students have written (or composed) their sentences based on the sentence frames, the class can write the definition of a triangle together:



