Two Wheels and a Belt
Task
A certain machine is to contain two wheels, one of radius 3 centimeters and one of radius 5 centimeters, whose centers are attached to points 14 centimeters apart. The manufacturer of this machine needs to produce a belt that will fit snugly around the two wheels, as shown in the diagram below. How long should the belt be?

IM Commentary
This task combines two skills from domain G-C: making use of the relationship between a tangent segment to a circle and the radius touching that tangent segment (G-C.2), and computing lengths of circular arcs given the radii and central angles (G-C.5). It also requires students to create additional structure within the given problem, producing and solving a right triangle to compute the required central angles (G-SRT.8).
Since the task is quite complex, it is more suitable for classroom work rather than assessment.
In solving the tasks there are decisions to be made about when to evaluate intermediate expressions. The solution given takes a middle path, leaving the $\arccos(2/14)$ unevaluated until the length of each component is evaluated. Evaluating this function prematurely can lead to accumulation of rounding error.
Solution
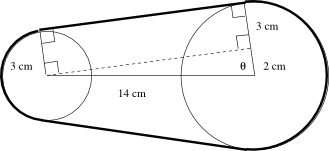
The length of the belt consists of four parts: two segments tangent to the two circles, and two circular arcs.
To determine the length of the tangent segments, we draw a line from the center of the small circle perpendicular to the radius of the large circle. Since the radius of each circle is perpendicular to the tangent segment at the point of tangency, this forms a rectangle. The length of the tangent segment is equal to the length of the opposite side of the rectangle, which is a leg of a right triangle with a hypotenuse of 14 cm and another leg of length 2 cm. So the length of each tangent segment is $$ \mbox{Length} = \sqrt{14^2 - 2^2} = 8\sqrt{3} \mbox{ cm}. $$
To compute the lengths of the two circular arcs, we start by computing the angle $\theta$ in our right triangle: $$ \theta = \arccos \frac{2}{14}. $$ This is also the angle between the radius of the small wheel and the horizontal line joining the two centers in the diagram, and twice this angle is the central angle that subtends the circular arc on the small wheel. So the length of the part of the belt that is wrapped around the small wheel is approximately $$2 \arccos\frac{2}{14} \cdot 3 \approx 8.56 \ \text{cm}.$$
Meanwhile, the central angle that subtends the circular arc on the large wheel is $2\pi - 2\arccos\frac{2}{14}$ radians, and thus the length of the part of the belt that is wrapped around the large wheel is $$(2\pi - 2\arccos\frac{2}{14}) \cdot 5 \approx 17.14\ \text{cm}.$$
So the total length of the belt should be $$ 2 \cdot 8\sqrt{3} + 8.56 + 17.14 \approx 53.42 \mbox{ cm}. $$
Two Wheels and a Belt
A certain machine is to contain two wheels, one of radius 3 centimeters and one of radius 5 centimeters, whose centers are attached to points 14 centimeters apart. The manufacturer of this machine needs to produce a belt that will fit snugly around the two wheels, as shown in the diagram below. How long should the belt be?

