Setting Up Sprinklers
Task
Selina has a 9 meter by 12 meter lawn that she wants to water. She has two sprinklers, each of which can water grass within an 8.4-meter radius. Selina wants to set up the two sprinklers so that they are on corners of the lawn. She would like for the sprinklers to water as much of the lawn as possible, because she will have to manually water the part of the lawn that is not covered by the sprinklers.
- Selina considers two different strategies for placing the sprinklers. One strategy is to put the sprinklers at opposite ends of a 12-meter side of the lawn. The other is to put the sprinklers at opposite corners of the lawn. (See the figures below.) Which strategy appears to be best? Justify your answer.

- If Selina chooses the better of these two strategies, what percentage of the lawn will she be able to water with the sprinklers?
- If Selina is allowed to put sprinklers in the interior of her lawn, how many sprinklers does she need to water the entire lawn?
IM Commentary
This task involves several different types of geometric knowledge and problem-solving: finding areas of sectors of circles (G-C.5), using trigonometric ratios to solve right triangles (G-SRT.8), and decomposing a complicated figure involving multiple circular arcs into parts whose areas can be found (MP.7). It also engages students in some of the steps of the modeling cycle, in particular:
(2) formulating a model by creating and selecting geometric, graphical, tabular, algebraic, or statistical representations that describe relationships between the variables,
(3) analyzing and performing operations on these relationships to draw conclusions, and
(4) interpreting the results of the mathematics in terms of the original situation.
Teachers who wish to engage their students in some of the more creative aspects of modeling can just skip parts (a) and (b) of the task and have students jump into part (c).
Teachers who wish to use this problem as a classroom task may wish to have students work on the task in cooperative learning groups due to the high technical demand of the task. If time is an issue, teachers may wish to use the Jigsaw cooperative learning strategy to divide the computational demands of the task among students while requiring all students to process the mathematics in each part of the problem.
Solution
-
In both sprinkler placements, each sprinkler covers a 90-degree sector of a circle of radius 8.4 meters. However, in each placement, the areas covered by the two sprinklers overlap. The placement that produces the smallest area of overlap will cover more area overall, since the total area covered is equal to the sum of the areas of the two 90-degree sectors minus the overlap.

If we draw the areas covered by the sprinklers in each of the two placements, it appears as though the overlap is slightly smaller if we place the sprinklers at the two corners. We will compute the total area covered by each placement in order to confirm this. -
We'll start by computing the area covered if Selina puts the two sprinklers at opposite ends of a 12-meter side of the lawn.
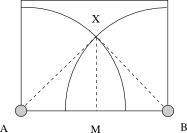
Let A and B be opposite ends of the 12-meter side of the lawn where the sprinklers are placed. Let X be the point where the two quarter-circles of radius 8.4 meters centered at A and B intersect, and let M be the foot of the perpendicular from X to side AB. (This is also the midpoint of AB.)
We'll decompose the area covered by the two sprinklers into the isosceles triangle ABX and two circular sectors (one in each circle). We know that AM = 6 meters and AX = 8.4 meters, so by the Pythagorean Theorem, XM $\approx$ 5.88 meters. So the area of triangle ABX is approximately $$ \mbox{Area} = \frac12 \cdot XM \cdot AB \approx \frac12 \cdot 5.88 \cdot 12 \approx 35.3 \mbox{ m}^2 . $$ The measure of angle XAM is $\arccos \frac{6}{8.4} \approx 44.4^\circ$. So the remainder of the covered area consists of two 45.6-degree sectors of circles of radius 8.4 meters. Each of these sectors has area $$ \mbox{Area} \approx \frac{90 - \arccos \frac{6}{8.4}}{360} \cdot \pi \cdot 8.4^2 \approx 28.1 \mbox{ m}^2. $$ So the total area covered is approximately 35.3 + 2(28.1) = 91.5 square meters, or about 84.7 percent of the lawn.
Now we compute the area covered if Selina places the sprinklers at opposite corners of the lawn:
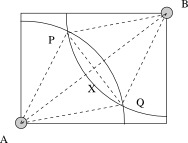
Let A and B be two opposite corners of the lawn, let P and Q be the two points at which quarter-circles of radius 8.4 meters centered at A and B intersect, and let X be the point at which the segments AB and PQ intersect. (This is also the center of the lawn.)
This time, we decompose the area covered into the rhombus APBQ and four circular sectors. The length of the diagonal AB is 15 meters by the Pythagorean Theorem, so AX = 7.5 meters. Since AP = 8.4 meters, by the Pythagorean Theorem, PX $= \sqrt{8.4^2 - 7.5^2}$ meters, and thus PQ $= 2\sqrt{8.4^2 - 7.5^2} \approx$ 7.57 meters. So the area of rhombus APBQ is $$ \mbox{Area} = \frac12 \cdot AB \cdot PQ \approx \frac12 \cdot 15 \cdot 7.57 \approx 56.8 \mbox{ m}^2. $$ Since $m\angle PAX = \arccos \frac{7.5}{8.4}$, the measure of angle PAQ is approximately $2\arccos \frac{7.5}{8.4} \approx$ 53.5 degrees. So the two sectors of circle A not covered by the rhombus add up to a 36.5-degree sector of a circle of radius 8.4 meters. The same is true of the two sectors of circle B not covered by the rhombus, so the remaining area is equivalent to approximately a 73.0-degree sector of a circle of radius 8.4 meters: $$ \mbox{Area} \approx \frac{73.0}{360} \cdot \pi \cdot 8.4^2 \approx 44.9 \mbox{ m}^2. $$ So the total area covered by the sprinklers in this case is approximately 56.7 + 44.9 = 101.6 square meters, or about 94.1 percent of the lawn. This confirms that the strategy of placing the sprinklers at opposite corners of the lawn is significantly better. - It is in fact possible to water the entire lawn with one sprinkler if we are allowed to place sprinklers in the interior of the lawn. Suppose we place one sprinkler in the center of the lawn. Then the corners of the rectangle are $\sqrt{4.5^2 + 6^2} = 7.5$ meters away, which is smaller than the sprinkler's reach. Since the corners of a rectangle are the points farthest from the center, one sprinkler placed in the center can water the entire lawn.
Setting Up Sprinklers
Selina has a 9 meter by 12 meter lawn that she wants to water. She has two sprinklers, each of which can water grass within an 8.4-meter radius. Selina wants to set up the two sprinklers so that they are on corners of the lawn. She would like for the sprinklers to water as much of the lawn as possible, because she will have to manually water the part of the lawn that is not covered by the sprinklers.
- Selina considers two different strategies for placing the sprinklers. One strategy is to put the sprinklers at opposite ends of a 12-meter side of the lawn. The other is to put the sprinklers at opposite corners of the lawn. (See the figures below.) Which strategy appears to be best? Justify your answer.

- If Selina chooses the better of these two strategies, what percentage of the lawn will she be able to water with the sprinklers?
- If Selina is allowed to put sprinklers in the interior of her lawn, how many sprinklers does she need to water the entire lawn?
