Dilating a Line
Task
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below.

- In the picture, locate the images A', B', and C' of the points A, B, and C under this dilation.
- Based on your picture in part (a), what do you think happens to the line l when we perform the dilation?
- Based on your picture in part (a), what appears to be the relationship between the distance A'B' and the distance AB? How about the distances B'C' and BC?
- Can you prove your observations in part (c)?
IM Commentary
When working on this classroom task, students should be provided with a separate copy of the picture (or more space should be provided below the picture) so that they can draw the points A', B', and C'.
Standard G-SRT.1 asks students to "Verify experimentally" that a dilation takes a line that does not pass through the center to a line parallel to the original line, and that a dilation of a line segment (whether it passes through the center or not) is longer or shorter by the scale factor. This task gives students the opportunity to verify both of these facts for a specific example. It may be helpful to provide students with rulers so that they can measure and duplicate lengths without having to perform formal constructions.
Part (d) of this task gives students an opportunity to prove that lengths of line segments get doubled under this particular dilation, though it is important to note that the particular proof given here only works when the scale factor is 2. This task engages standard G-CO.10. A teacher who wishes to skip this part may do so without losing significant work on G-SRT.1.
Solution
-
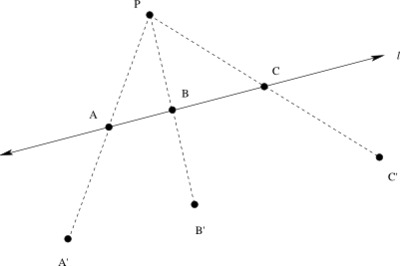
To locate the point A', we draw a line segment from P to A, and extend the line segment through A. We place A' on this line so that the distance from P to A' is twice the distance from P to A. We locate B' and C' using a similar procedure. -
The points A', B', and C' appear to be collinear. If we choose more points on l and dilate those points about point P, we will see that the dilations of those points also appear to lie on the line through A', B', and C'. It appears that the dilations of the points on the line l form a new line l' that is parallel to line l:

- In the picture, it appears that A'B' = 2AB, and B'C' = 2BC. We can obtain more evidence for this guess by measuring the lengths of the segments in our picture.
-
We will prove that A'B' = 2AB; the proof that B'C' = 2BC is similar. Note that we will prove this fact without using our unproven conjecture that the dilation of line l is a line parallel to l. (Note to teacher: Allowing students to use this fact makes this proof an easier, but still very worthwhile, classroom exercise.)
We begin by drawing a line through A parallel to line PB, and a line through B parallel to line PA. Let these lines meet at X. Note that we do not yet know that X is on the line A'B'; we will show this in our proof.

Since PAXB is a parallelogram, we know that AX = PB, BX = PA, and angle AXB is congruent to angle BPA.
Now we turn our attention to triangle AA'X. We know that angle A'AX is congruent to angle APB since lines AX and PB are parallel. We also know that AA' = PA, and AX = PB, so by SAS congruence, triangle AA'X is congruent to triangle PAB. Thus the angle AXA' is congruent to angle PBA. A similar argument shows that triangle BXB' is congruent to triangle PAB, and therefore angle BXB' is congruent to angle PAB.
Now we know that $$ m\angle A'XA + m\angle AXB + m\angle BXB' = m\angle PAB + m\angle APB + m\angle PBA = 180^\circ. $$ Thus the angle $\angle A'XB'$ is a straight angle, and we now know that X lies on the line A'B'.
The congruence of triangles PAB, AA'X, and BXB' shows that AB = A'X = XB'. Since X lies on line A'B', we know that A'B' = A'X + XB' = AB + AB = 2AB. This is what we wanted to show.
Dilating a Line
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below.

- In the picture, locate the images A', B', and C' of the points A, B, and C under this dilation.
- Based on your picture in part (a), what do you think happens to the line l when we perform the dilation?
- Based on your picture in part (a), what appears to be the relationship between the distance A'B' and the distance AB? How about the distances B'C' and BC?
- Can you prove your observations in part (c)?
