Comparing Snow Cones
Task
Pablo's Icy Treat Stand sells home-made frozen juice treats as well as snow-cones. Originally, Pablo used paper cone cups with a diameter of 3.5 inches and a height of 4 inches.

His supply store stopped carrying these paper cones, so he had to start using more standard paper cups. These are truncated cones (cones with the "pointy end" sliced off) with a top diameter of 3.5 inches, a bottom diameter of 2.5 inches, and a height of 4 inches.

Because some customers said they missed the old cones, Pablo put a sign up saying "The new cups hold $50\%$ more!" His daughter Letitia wonders if her father's sign is correct. Help her find out.
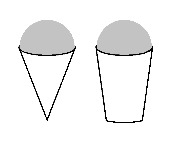
How much juice can cup A hold? (While cups for juice are not usually filled to the top, we can assume frozen juice treats would be filled to the top of the cup.)
How much juice can cup B hold?
By what percentage is cup B larger in volume than cup A?
Snow cones have ice filling the cup as well as a hemisphere of ice sticking out of the top of each cup. How much ice is in a snow cone for each cup?
By what percentage is the snow cone in cup B larger than the snow cone in conical cup A?
Is Pablo's sign accurate?
IM Commentary
Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.)
There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller.
Algebraically, we can call the volume of the truncated conical cup $T$, the volume of the conical cup $C$ and the volume of the snow dome $D$. So from the computations in the solution we have, for example, that $\frac{T}{C}$ is roughly $2.23$.
But we only need to know that $T \ge C$ or $\frac{T}{C} \ge 1$, to deduce that $\frac{T + D}{C + D} \le \frac{T}{C}$. To see this we compare $$(T+ D) \times C = TC + DC$$ with $$T \times (C + D) = TC + TD,$$ and see the latter is larger because $CD \le TD$, which we know because $C\le T$. Because the ratio has decreased when adding $D$ to the numerator and denominator, the percentage difference has also decreased.
Indeed, if the "dome" part were even larger, the percentage increase would be smaller. If the dome were large enough, Pablo's sign would need to be changed (in reference to the snow cones) because there would be less than $50\%$ more in the truncated cone cup.
Submitted by Michelle Mourtgos of Grantsville Junior High School to the fourth Illustrative Mathematics Task Writing Contest.
Solution
-
Volume of conical cup A
Let $d$ be the diameter, $r$ the radius, and $h$ the height of the cone. Then the volume $v$ is: $$v = \frac13 \pi r^2 h$$ Using the values given in the problem, we have: $$ \begin{align} d &= 3.5 \text{ in} \\ h &= 4 \text{ in} \\ r &= \frac{d}{2} = \frac{3.5}{2} = 1.75 \text{ in} \\ \\ \\ \text{Volume of Cup} &= \frac13(3.14)(1.75)^2(4) \approx 12.82 \end{align} $$ So the volume of conical cup A is $12.82 \text{ in}^3$.
-
To find the volume of the truncated conical cup B, we need to find the volume of the large cone and the smaller cone that is cut off to make the truncated cone, and then subtract to find its volume.

If $h$ is the height of the smaller cone that is cut off, then $h+4$ is the height of the larger cone. To find the heights of the larger cone and the smaller cone, we can slice through the central axis of the larger cone to see an isosceles triangle.

Since there are two triangles with congruent angles, we know they are similar and that the side lengths are proportional. If $h$ is the height of the smaller cone that is cut off, then $h+4$ is the height of the larger cone. We can write the equation $$\frac{h}{h+4} = \frac{1.25}{1.75}$$ which is equivalent to $$1.75h = 1.25h +1.25\cdot 4$$ which is equivalent to $$0.5h = 5.$$ So $h=10$, and the height of the large cone is $14$.
In the following formulas, we can distinguish the dimensions of the two cones by using lower case letters for the small cone and upper case letters for the larger code. For example, let $r$ represent the radius of the smaller cone and $R$ represent the radius of the larger cone. Then we can find the volumes of each cone and subtract the smaller from the larger:
$$ \begin{align} R &= \frac{3.5}{2} = 1.75 \text{ in} \\ r &= \frac{2.5}{2} = 1.25 \text{ in} \\ H &= 14 \\ h &= 10 \\ \\ \\ \text{Volume of Cup} &= V - v \\ &= \frac13 \pi R^2 H - \frac13 \pi r^2 h \\ &= \frac13(3.14)(1.75)^2(14) - \frac13(3.14)(1.25)^2(10) \\ &\approx 28.54 \end{align} $$ So the volume of cup B is $28.54 \text{ in}^3$. -
Percent Comparison of Volumes
$$\frac{28.54 – 12.82}{12.82} \approx 123\%$$The truncated conical cup B holds 123% more water than the conical cup A.
-
Volume of Snow Cone Dome
The volume of the dome is half the volume of a sphere, so $$\text{Volume of Dome} = \frac12(\text{Volume of Sphere}) = \frac23 \pi r^3 $$ $$ \begin{align} &d = 3.5 \text{ in} \\ &r = \frac{d}{2} = \frac{3.5}{2} = 1.75 \text{ in} \\ \\ &\text{Volume of Dome} = \frac23(3.14)(1.75)^3 \approx 11.22 \text{ in}^3 \\ \\ &\text{Volume of Conical Cup A with Snow Cone Dome} = 12.82 + 11.22 = 24.04 \text{ in}^3 \\ \\ &\text{Volume of Truncated Conical Cup B with Snow Cone Dome} = 28.54 + 11.22 = 39.76 \text{ in}^3 \end{align} $$
-
Percent Comparison of Snow Cones
$$\frac{39.76 – 24.04}{24.04} \approx 65\%$$The snow cone in the truncated conical cup has 65% more ice than the snow cone in the conical cup.
-
Accuracy of Pablo's sign
For neither frozen treat is Pablo's sign strictly mathematically accurate. But if a vendor of something like frozen treats is promising some percentage more and is actually providing a larger percentage increase, customers are usually pleased. So Pablo's sign is probably accurate enough for its purpose.
Comparing Snow Cones
Pablo's Icy Treat Stand sells home-made frozen juice treats as well as snow-cones. Originally, Pablo used paper cone cups with a diameter of 3.5 inches and a height of 4 inches.

His supply store stopped carrying these paper cones, so he had to start using more standard paper cups. These are truncated cones (cones with the "pointy end" sliced off) with a top diameter of 3.5 inches, a bottom diameter of 2.5 inches, and a height of 4 inches.

Because some customers said they missed the old cones, Pablo put a sign up saying "The new cups hold $50\%$ more!" His daughter Letitia wonders if her father's sign is correct. Help her find out.

How much juice can cup A hold? (While cups for juice are not usually filled to the top, we can assume frozen juice treats would be filled to the top of the cup.)
How much juice can cup B hold?
By what percentage is cup B larger in volume than cup A?
Snow cones have ice filling the cup as well as a hemisphere of ice sticking out of the top of each cup. How much ice is in a snow cone for each cup?
By what percentage is the snow cone in cup B larger than the snow cone in conical cup A?
Is Pablo's sign accurate?
