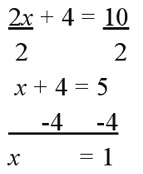Solving Equations
Task
In elementary school, students often draw pictures of the arithmetic they do. For instance, they might draw the following picture for the problem $2 + 3$:
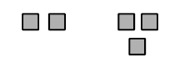
In this picture, each square represents a tile.
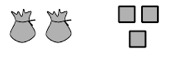
We can do the same thing for algebraic expressions, but we need to be careful about how we represent the unknown. If we assume that an unknown number of tiles $x$ are contained in a bag, we could draw the following picture for $2x + 3$:
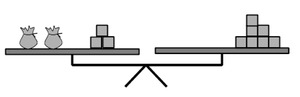
When we have an equation to solve, we assume that the two sides of the equation are equal. We can represent this by showing them level on a balance. For example, we the equation $2x + 3 = 7$ could be shown as:
When we solve equations, we can add, subtract, multiply or divide both sides of the equation by the same thing in order to maintain the equality. This can be shown in pictures by keeping the balance level. For example, we could solve the equation $2x + 3 = 7$ using pictures by first removing (subtracting) 3 from each side, and then splitting (dividing) the remaining blocks into two equal groups:

From this picture, we can see that, in order to keep the balance level, each bag must contain 2 tiles, which means that $x = 2$.
-
Solve $5x + 1 = 2x + 7$ in two ways: symbolically, the way you usually do with equations, and also with pictures of a balance. Show how each step you take symbolically is shown in the pictures.
-
Solve the equation $4x = x + 1$ using pictures and symbols. Discuss any issues that arise.
-
What issues arise when you try to solve the equation $2 = 2x - 4$ using pictures? Do the same issues arise when you solve this equation symbolically?
-
Make up a linear equation that has no solutions. What would happen if you solved this equation with pictures? How is this different than an equation that has infinitely many solutions?
Use pictures to show why the following solution to the equation $2x + 4 = 10$ is incorrect:
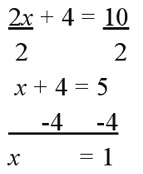
Solution
-

-
When you solve this equation with pictures, you end up with 3 bags balancing with 1 tile. In order to do the division, you have to cut the tile, leading to the fraction 1/3, which is the solution you get symbolically.
-
In order to solve this equation with pictures, you have to have some way of representing the subtraction in $2x – 4$. If students have experience with integer chips, they can transfer that knowledge to this situation to show $2x + -4$, but otherwise they may struggle with the idea. The pictures give us a nice model for understanding the operations we do to solve equations, but it is only smooth for problems with “nice†numbers. This is one reason why we want to move to the symbolic approach.
-
A linear equation will have no solution if there are the same number of $x$’s and different constants on each side. For example: $2x + 4 = 2x + 1$. If you solve this with pictures, when you take away the $2x$ from both sides you will end up with $4 = 1$, which clearly cannot be balanced. If the equation had infinitely many solutions, you would find that you had exactly the same picture on the two sides of the balance.
-
The mistake is in the first step - the student divided only part of the left-hand-side of the equation by 2. You can see in the picture that splitting the equation this way will not keep the balance level (assuming the two bags are equal):

Solving Equations
In elementary school, students often draw pictures of the arithmetic they do. For instance, they might draw the following picture for the problem $2 + 3$:

In this picture, each square represents a tile.
We can do the same thing for algebraic expressions, but we need to be careful about how we represent the unknown. If we assume that an unknown number of tiles $x$ are contained in a bag, we could draw the following picture for $2x + 3$:

When we have an equation to solve, we assume that the two sides of the equation are equal. We can represent this by showing them level on a balance. For example, we the equation $2x + 3 = 7$ could be shown as:

When we solve equations, we can add, subtract, multiply or divide both sides of the equation by the same thing in order to maintain the equality. This can be shown in pictures by keeping the balance level. For example, we could solve the equation $2x + 3 = 7$ using pictures by first removing (subtracting) 3 from each side, and then splitting (dividing) the remaining blocks into two equal groups:

From this picture, we can see that, in order to keep the balance level, each bag must contain 2 tiles, which means that $x = 2$.
-
Solve $5x + 1 = 2x + 7$ in two ways: symbolically, the way you usually do with equations, and also with pictures of a balance. Show how each step you take symbolically is shown in the pictures.
-
Solve the equation $4x = x + 1$ using pictures and symbols. Discuss any issues that arise.
-
What issues arise when you try to solve the equation $2 = 2x - 4$ using pictures? Do the same issues arise when you solve this equation symbolically?
-
Make up a linear equation that has no solutions. What would happen if you solved this equation with pictures? How is this different than an equation that has infinitely many solutions?
Use pictures to show why the following solution to the equation $2x + 4 = 10$ is incorrect: