Adding Multiples
Task
Nina was finding multiples of 6. She said,
18 and 42 are both multiples of 6, and when I add them, I also get a multiple of 6: $$18+42 = 60.$$
Explain to Nina why adding two multiples of 6 will always result in another multiple of 6.
Â
IM Commentary
This task is appropriate for assessing student’s understanding of repeated reasoning and generalizing that understanding to prepare them for deeper algebraic thinking needed in the expressions and equations domain. It will allow the teacher to assesses the level of understanding by analyzing how they solved the problem whether algebraically, concretely with picture representations or both. Those students who solved it more concretely may benefit from teacher guidance to the general algebraic solution. Â
The Standards for Mathematical Practice focus on the nature of the learning experiences by attending to the thinking processes and habits of mind that students need to develop in order to attain a deep and flexible understanding of mathematics. Certain tasks lend themselves to the demonstration of specific practices by students. The practices that are observable during exploration of a task depend on how instruction unfolds in the classroom. While it is possible that tasks may be connected to several practices, the commentary will spotlight one practice connection in depth. Possible secondary practice connections may be discussed but not in the same degree of detail.
This task helps illustrate Mathematical Practice 8, Look for and express regularity in repeated reasoning. When students demonstrate MP.8, they notice if calculations are repeated, and look both for general methods and for shortcuts. They are asked to generalize why when adding two multiples of a number (6 in this case) will always result in another multiple of the same number (6). This task would be most useful to assess the students depth of understanding in generalizing repeated calculations (MP.8) and applying the distributive property to show that two numbers with a common factor can be expressed as a multiple of a sum of two whole numbers with no common factor. This could be accomplished by having students work independently on this task after multiple opportunities to solve similar problems dealing with multiples, factoring and the distributive property. The students could then share their solutions with other students and discuss similarities and differences in their solutions, finalizing their answers making sure to explain their thinking with numbers and context. The teacher could use these solutions as a formative assessment to guide small groups of those students who are not seeing the benefit of MP.8 to solve this task, into seeing the generalizations that stem from it. This will be beneficial for all students as it is a “rehearsal†for algebra. Â
Solutions
Solution: Showing it with pictures.
18 and 42 are both multiples of 6 which means 6 is a factor of both numbers. $$6 \cdot 3 = 18$$ $$ 6 \cdot 7 = 42$$
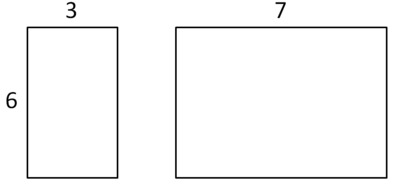
When you add 18 and 42, you can use the distributive property to show that the sum is also a multiple of 6: $$6 \cdot 3 + 6 \cdot 7 = 6 \cdot (3 + 7) = 6 \cdot 10$$
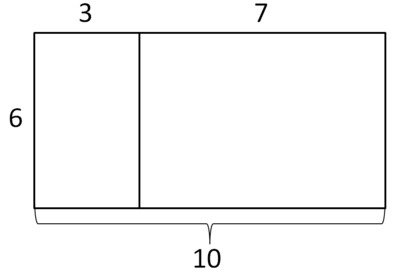
If you have any two multiples of 6, you can write them both as 6 times a whole number. Using the distributive property, their sum will also be 6 times a whole number, just like in the example of 18 and 42.
Solution: An algebraic explanation that aligns with 6.EE.2
18 and 42 are both multiples of 6 which means 6 is a factor of both numbers. $$6 \cdot 3 = 18$$ $$ 6 \cdot 7 = 42$$ When you add 18 and 42, you can use the distributive property to show that the sum is also a multiple of 6: $$6 \cdot 3 + 6 \cdot 7 = 6 \cdot (3 + 7) = 6 \cdot 10$$ If you have any two multiples of 6, you can write them both as 6 times a whole number. We can write this in symbols as $$6\cdot a$$ $$6\cdot b$$ (where $a$ and $b$ are both whole numbers). When you add them, you have $$ 6\cdot a + 6\cdot b = 6 \cdot (a+b)$$ Since $a$ and $b$ are whole numbers, so is $a+b$. So the sum of two multiples of 6 is always a multiple of 6.
Please note that there is nothing special about 6 in this argument, so it will work exactly the same way with any whole number in place of 6.
Adding Multiples
Nina was finding multiples of 6. She said,
18 and 42 are both multiples of 6, and when I add them, I also get a multiple of 6: $$18+42 = 60.$$
Explain to Nina why adding two multiples of 6 will always result in another multiple of 6.
Â
