Last Person Standing
Task
An instructor in a classroom of 40 students gave each of the 40 students a bag of 10 chips. In each bag, some of the 10 chips were red, and the rest were white. The bags were made of a thick cloth so that no one could see inside the bags, and all of the bags were identical in terms of their contents.
 Each student was asked to remove one chip from his or her bag and to raise his or her hand if that chip was red.  (This constitutes one “round†of the game.) Those who selected a red chip were allowed to remain in the game and play another round; those who selected a white chip were “out†of the game. Each student who was still in the game was asked to place his/her chip back into the bag and to repeat the selection process when asked. This continued until there was only one student left.
1) If you were told that each bag contained 6 red chips and 4 white chips, what is the expected number of students who would raise their hands in the first round of this game?
2)Â Assuming that each bag contained 6 red chips and 4 white chips, fill in the table below indicating how many students you would expect to raise a hand in each round. Â (Note: it is ok to have a non-integer expected number of students in any round of the models you are developing.)
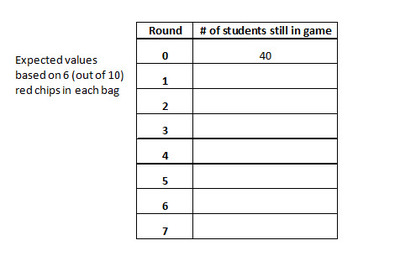
3) The following represent the actual results from the classroom.

At the end of the game, the instructor asked “Knowing that each bag has 10 chips, and knowing that everyone’s bags are the same, how many red chips do you believe are in each bag?â€
a) Develop a table similar to the one you made in part 2 above based on the assumption of 5 red chips in a bag.  Make a second table based on the assumption of  7 red chips in a bag.


b) Based on the actual results and the 3 models you have developed, do you believe that each bag had 5, 6, or 7 red chips? Choose one value and explain.
Â
IM Commentary
This exercise is intended to have students consider and model what we would formally call “exponential decay†and to compare observed data to what is expected under a given model (S-IC.A.2). The assumption is that the outcome for each student in any given round is independent of the outcomes for the other students and that the rounds are independent of one another. It is also assumed that the probability of success or failure is the same for every student and does not change from round to round.  This is why it is important to have students replace their selected chips back into their bags before drawing again.
Students may have previously encountered geometric progressions in terms of exponential decay, or perhaps this is their first time, and some general explanation or review is warranted. In the first questions, students should be able to develop the expected model for each round based on multiplying the expected number of remaining students from the previous round by 0.60. Students then follow a similar procedure to develop the expected models for 50% and 70% respectively. One of the more important statistical points in this task is that observed data  do not always exactly follow an assumed model perfectly.
Solution
1) The chance of selecting “red†is 60%, so 40 *.6 = 24
2)

3) a.
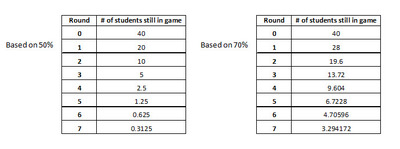
b.  Anticipate that students will say that they think that the number of red chips in the bag is 6. The explanations that students give for choosing this model will vary, but look for the following key points:
- The actual first round value of “26†would be unusual if the P(red) = .50.
- In the actual results, each subsequent round’s “number of students still in game†value is closest to 60% of the previous round’s value (as opposed to 50% or 70%).
- The actual values of “number of students still in game†(particularly in the later rounds) most closely follow the 60% model’s expectations.
- In the actual game, a winner was crowned after 7 rounds. This best matches the 60% model. The winner would most likely be determined after fewer rounds in a 50% situation (and likewise, more rounds would most likely be required for a 70% situation).
Last Person Standing
An instructor in a classroom of 40 students gave each of the 40 students a bag of 10 chips. In each bag, some of the 10 chips were red, and the rest were white. The bags were made of a thick cloth so that no one could see inside the bags, and all of the bags were identical in terms of their contents.
 Each student was asked to remove one chip from his or her bag and to raise his or her hand if that chip was red.  (This constitutes one “round†of the game.) Those who selected a red chip were allowed to remain in the game and play another round; those who selected a white chip were “out†of the game. Each student who was still in the game was asked to place his/her chip back into the bag and to repeat the selection process when asked. This continued until there was only one student left.
1) If you were told that each bag contained 6 red chips and 4 white chips, what is the expected number of students who would raise their hands in the first round of this game?
2)Â Assuming that each bag contained 6 red chips and 4 white chips, fill in the table below indicating how many students you would expect to raise a hand in each round. Â (Note: it is ok to have a non-integer expected number of students in any round of the models you are developing.)

3) The following represent the actual results from the classroom.

At the end of the game, the instructor asked “Knowing that each bag has 10 chips, and knowing that everyone’s bags are the same, how many red chips do you believe are in each bag?â€
a) Develop a table similar to the one you made in part 2 above based on the assumption of 5 red chips in a bag.  Make a second table based on the assumption of  7 red chips in a bag.


b) Based on the actual results and the 3 models you have developed, do you believe that each bag had 5, 6, or 7 red chips? Choose one value and explain.
Â
