Visualizing Completing the Square
Task
Enrico has discovered a geometric technique for ''completing the square'' to find the solutions of quadratic equations. To solve the equation $x^2 + 6x + 4 = 0$, Enrico draws a square of dimension $x$ by $x$ and attaches 6 strips (3 of dimension 1 by $x$ and 3 of dimension $x$ by 1) to make the picture below:
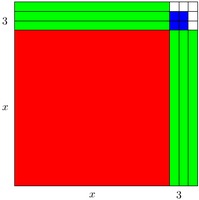
To complete the larger square, Enrico adds 9 squares of dimension 1 by 1. He has 4 of them in his initial expression so he needs five more as shown in the picture. So the picture represents the equation $$ (x+3)^2 = (x^2 + 6x + 4) + 5 $$
- Explain how Enrico's method helps find the roots of $x^2 + 6x + 4 = 0$.
- Help Enrico draw a picture for, and then solve, the equation $x^2 - 6x + 4 = 0$.
IM Commentary
The purpose of this task is to help provide geometric intuition for the algebraic process called ''completing the square.'' This is often done to help solve quadratic equations but the reason why the process is called completing the square is usually not highlighted. It turns out that when the algebraic expressions are modeled geometrically we find part of a square which is missing a small piece in order to be complete. For the two quadratic equations considered here, the roots are real. This process applies to all quadratic equations, however, and is one of the best known methods for deriving the quadratic formula. If students are comfortable with the examples given here, the teacher might want to explore what happens when the coefficients of the quadratic equation are variables (and hence work toward deriving the quadratic formula).
Solution
-
To solve the equation $(x^2 + 6x + 4) = 0$ using $(x+3)^2 = (x^2 + 6x + 4) + 5$, Enrico can proceed as follows. The second equation can be rewritten as $$ x^2 + 6x + 4 = (x+3)^2 - 5. $$ So the solutions of $x^2 + 6x + 4 = 0$ are the same as the solutions to $(x+3)^2 - 5 = 0$. We can add 5 to both sides obtaining $$ (x+3)^2 = 5 $$ and then taking a square root on both sides gives $$ |x+3| = \sqrt{5}. $$ This has solutions $x = -3 + \sqrt{5}$ and $x = -3 - \sqrt{5}$.
-
For the equation $x^2 - 6x + 4 = 0$ we can still start with an $x$ by $x$ square representing $x^2$. But this time we want to take away $3x$ from each side of the square. We can do this as in the picture below but we have taken away the 9 small squares (where the rectangles of area $x$ intersect) twice.

This means that the small square, of dimensions $x-3$ by $x-3$ is equal to the big square minus the 6 rectangles of dimension $x$ by $1$ plus 9 (to account for the second time these 9 squares are taken away). In equation form: $$ (x-3)^2 = x^2 - 6x + 9. $$ From here we find $$ (x-3)^2 - 5 = x^2 - 6x + 4. $$ Solving as we did in part (a) we find that $x = 3+\sqrt{5}$ and $x = 3-\sqrt{5}$ are the two roots of the quadratic equation $x^2 - 6x + 4 = 0$.
Visualizing Completing the Square
Enrico has discovered a geometric technique for ''completing the square'' to find the solutions of quadratic equations. To solve the equation $x^2 + 6x + 4 = 0$, Enrico draws a square of dimension $x$ by $x$ and attaches 6 strips (3 of dimension 1 by $x$ and 3 of dimension $x$ by 1) to make the picture below:

To complete the larger square, Enrico adds 9 squares of dimension 1 by 1. He has 4 of them in his initial expression so he needs five more as shown in the picture. So the picture represents the equation $$ (x+3)^2 = (x^2 + 6x + 4) + 5 $$
- Explain how Enrico's method helps find the roots of $x^2 + 6x + 4 = 0$.
- Help Enrico draw a picture for, and then solve, the equation $x^2 - 6x + 4 = 0$.
