The Circumference of a Circle and the Area of the Region it Encloses
Task
- What is the definition of a circle with center $A$ and radius $r$?
-
A circle has center $A$ and radius $AB$. Is point $A$ on the circle? Is point $B$ on the circle? Explain.

-
Imagine that a circle with center $A$ is drawn on 1/4 inch grid paper as shown below. What is the radius of the circle?

- Use the grid to estimate the circumference of the circle.
- Use the grid to estimate the area of the region enclosed by the circle.
- What are you measuring when you find the circumference of a circle? What are you measuring when you find the area of a circle?
IM Commentary
A circle is the set of points that are a specified distance $r$ from some fixed point $P$ called the center of the circle. The purpose of this task is to help students differentiate between a circle and the region inside of the circle so that they understand what is being measured when the circumference and area are being found. This task is best used as a lead-in to the formulas for circumference and area of a circle.
It is common for students to get confused about which parts of a figure are part of the circle itself (i.e. the curve that represents the set of points a fixed distance from the center) and which are just defined by the circle (i.e. the region inside it). In particular, many students are unsure about whether the center of the circle is part of the circle. Even though the center is required for the definition of the circle, it isn't actually contained in the circle itself.
To distinguish between a circle and the region it encloses, we can talk about a circle and a disk. An open disk is the set of points in the interior of a circle (but not including the circle); a closed disk is the circle plus all the points inside it; see the picture below.
 One reason that students get confused about the difference between a circle and a its interior is that we ask them to "Find the circumference and area of the circle," when in fact we mean, "Find the circumference of the circle and the area of the region it encloses." This use of language is common and expected, so teachers just need to be aware of the potential for confusion. This task provides a good opportunity to address MP6, Attend to precision.
One reason that students get confused about the difference between a circle and a its interior is that we ask them to "Find the circumference and area of the circle," when in fact we mean, "Find the circumference of the circle and the area of the region it encloses." This use of language is common and expected, so teachers just need to be aware of the potential for confusion. This task provides a good opportunity to address MP6, Attend to precision.
In the Common Core, students start studying area and perimeter in 3rd grade, and should be grappling with the distinction between a simple closed curve and the region it encloses even then; see 3.MD Shapes and their Insides.
The circle in part (c) has a radius of 1 inch so that the area is $\pi$ and the circumference is $2\pi$. The choice of 1/4-inch grid paper (which can be used if the teacher wants the figures to be actual size) is chosen so that it is possible to get reasonably good estimates of the circumference and perimeter without making the work required too tedious.
Solution
- A circle with center $A$ and radius $r$ is the set of all points in the plane that are $r$ units away from $A$.
- Even though point $A$ is the center of the circle, it is not actually part of the circle because it is 0 units from itself and $AB$ is greater than 0 units long. $B$ is on the circle by definition, since the radius of the circle is the the length of the line segment that joins point $A$ and point $B$, so $B$ is a distance of $AB$ from $A$.
-
The red octagon superimposed on the circle below has side lengths that are a little longer than $\frac34$ of an inch (they are the hypotenuse of a right triangle with legs $\frac34$ inch and $\frac14$ inch).
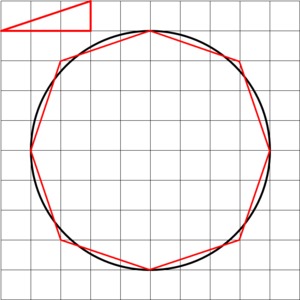
Since there are 8 of them, their total length is a little longer than $8\cdot\frac34$ inches, or a little bit longer than 6 inches.
-
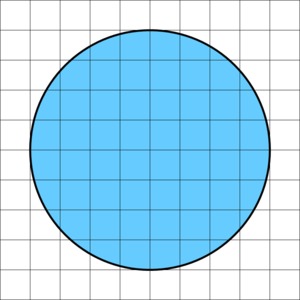
The area of the circle is the number of square inches that are contained in the interior of the circle; in other words, the area of the blue region shown below.
If we shade all of the squares that are completely contained in the interior light blue and all the squares beyond that that completely contain the circle in a darker shade of blue, we can get an upper and lower bound for the area of the circle.
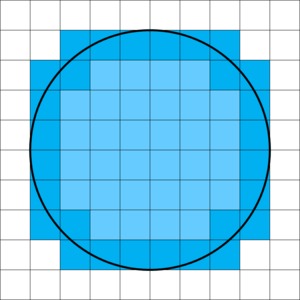
There are 32 small squares completely contained in the interior and each has an area of $\frac14\cdot\frac14=\frac{1}{16}$ square inches. So their combined area is $\frac{32}{16}=2$ square inches. So the area of the circle is greater than 2 square inches.
There are 28 additional small squares for a total of 50 that completely contain the circle. $\frac{60}{16}=3\frac34$ square inches.
Thus, the area of the circle is greater than 2 and less than 3.75 square inches.
It is possible to get a much better estimate using triangles.
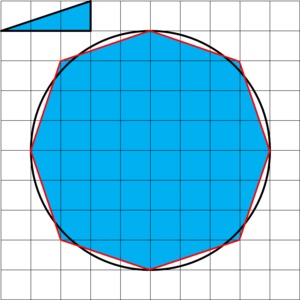
Using the polygon we used to estimate the perimeter, we get the area is close to $\frac{48}{16}=3$ square inches. It looks like this polygon slightly under-estimates the area, which is in fact the case.
-
The circumference of a circle is the length of the curve that is the circle itself. The area of a circle is the area of the region inside the circle.
The Circumference of a Circle and the Area of the Region it Encloses
- What is the definition of a circle with center $A$ and radius $r$?
-
A circle has center $A$ and radius $AB$. Is point $A$ on the circle? Is point $B$ on the circle? Explain.

-
Imagine that a circle with center $A$ is drawn on 1/4 inch grid paper as shown below. What is the radius of the circle?

- Use the grid to estimate the circumference of the circle.
- Use the grid to estimate the area of the region enclosed by the circle.
- What are you measuring when you find the circumference of a circle? What are you measuring when you find the area of a circle?
