Basketball Bounces, Assessment Variation 1
Task
SCREEN I
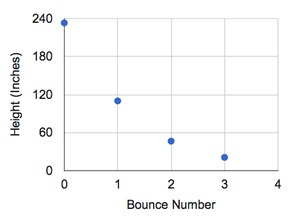
In science class, some students dropped a basketball and allowed it to bounce. They measured and recorded the highest point of each bounce.
The students’ data is shown in the table and scatterplot. The first data point ($n = 0$) represents the height of the ball the moment the students dropped it.
|
Bounce Number $n$ |
Measured Height in Inches $h(n)$ |
|---|---|
| 0 | 233 |
| 1 | 110 |
| 2 | 46.6 |
| 3 | 21 |
In this task, you will choose a function to model the data and use the model to answer some questions.
SCREEN II
a. Compute the first three values in the last column of the table below.
|
Bounce Number $n$ |
Measured Height in Inches $h(n)$ |
Factor by which Bounce Height Decreased $h(n-1)\div h(n)$ |
|---|---|---|
| 0 | 233 | |
| 1 | 110 | [____________] |
| 2 | 46.6 | [____________] |
| 3 | 21 | [____________] |
[Student could choose to open up a scientific calculator.]
SCREEN III
b. Let $n$ be the bounce number and $h(n)$ be the height. Consider the following general forms for different kinds of models where $a$ and $b$ represent numbers:
| Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|
| $h(n) = a\cdot n+b$ | $h(n) = a\cdot n^2+b$ | $h(n) = \frac{a}{n} +b$ | $h(n) = a\cdot e^{bn}$ |
Which of the models shown is most appropriate to use for the given data?
Given the data above, what are reasonable values for $a$ and $b$ if we want to create a specific model to fit the data? Write the appropriate values in the equation below.
[Based on the choice students make above, they are given the appropriate template below. Here is the template for the exponential model]

c. Based on your model, what will be the first bounce with a maximum height that is less than 1 inch?
[When the student clicks "Next" from this screen, they get a message, "Are you sure you are ready to go on? You cannot change any of your previous answers after you continue from this screen."]
SCREEN IV
d. Mika said,
The model I came up with is $h(n) = 233 \cdot e^{-0.8n}$. I used it to predict that after 50 bounces, the height of the bounces will be less than a thousandth of an inch. It is good to have the model because it would be very difficult to measure such small heights.
What is the best way to characterize Mika's claim?
- Mika's claim is true. The whole point of using models is to make predictions.
- Mika's claim is true but she should give a more precise bound for the height of the ball after 50 bounces because the heights will be much much smaller than one thousandth of an inch.
- Mika is correct that the model predicts that the bounces will all be less than a thousandth of an inch, but in reality the ball will be at rest before it has bounced 50 times.
- Mika is not using the model appropriately. Models can't be used to make predictions past the given data, only between data points.
- Mika is not using the model appropriately. The model doesn't fit the data very well so it can't be used to make predictions that far in the future.
- Mika's claim is not true. The model states that the ball will be at rest before it gets to 50 bounces so the bounce heights will be zero, which is easy to measure.
Done
IM Commentary
This task is part of a joint project between Student Achievement Partners and Illustrative Mathematics to develop prototype machine-scorable assessment items that test a range of mathematical knowledge and skills described in the CCSSM and begin to signal the focus and coherence of the standards.
Task Purpose
The purpose of this task is to assess aspects of students’ modeling skills in the context of standards
F-LE.1 Distinguish between situations that can be modeled with linear functions and with exponential functions
c. Recognize situations in which a quantity grows or decays by a constant percent rate per unit interval relative to another.F-LE.2 Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
This task asks students to analyze a set of data from a physical context, choose a model that reasonably fits the data, and use the model to answer questions about the physical context. This variant of the task is scaffolded; for a less scaffolded version, see F-LE Basketball Bounces, Assessment Variation 2
Cognitive Complexity
Mathematical Content
In this version of the task, students are guided to use the knowledge that exponential functions grow by equal factors over equal intervals. Students are asked to determine the quotient of consecutive terms of the given sequence (and should see that the quotients are close to one another). This should suggest to students who understand exponential functions that such a function is the best fit.
Of the model choices given, the linear and exponential models will likely be most familiar to students; the quadratic and rational models may be less familiar. However, the quadratic model can be eliminated because a parabola with its vertex on the vertical axis cannot fit the data, and the rational model because it is undefined at zero.
Part (c) requires students to solve an inequality $ae^{bn} \lt 1$ for $n$. This can be done by solving the equation $ae^{bn} = 1$ and thinking contextually to see that the minimal number of bounces needs to be greater than or equal to the solution to this equation. Note that the model must have a base of 2, 10, or $e$ because students only need to solve exponential functions using logarithms with these bases (see F-LE.4) and it is important for this solution approach to be available to them. The fact that the base is $e$ rather than 2 or 10 increases the complexity of the task.
Mathematical Practice
This task directly assesses MP 4:
- Students are required to decide which of several types of models is most reasonable in a real-world situation.
- After deciding, students must use data to specify the parameters in the model.
- Once the model is specified, students must use the model to solve a problem about the situation.
- Students will have the opportunity to return to a previous step (e.g., the step where the template is selected) if they find that their model does not make sense; for example, if the model predicts that the ball's bounce heights will never drop to less than an inch; or if it returns outputs inconsistent with those given in the table.
The last question also addresses MP 3 because students must critique a student’s claim and evaluate different possible counter claims for the one that is most accurate.
Linguistic Demand
The video of the bouncing ball decreases the linguistic complexity of the first part of the task, although the last part of the task has a high level of linguistic demand.
Stimulus Material
The stimulus material is complex, consisting of a video, a table, a graph, and a set of equations.
Response Mode
The response mode has a medium level of complexity as it requires students to use a drop-down menu and fill in the blanks to choose the parameters of the function.
Solution
a.
|
Bounce Number $n$ |
Measured Height in Inches $h(n)$ |
Factor by which Bounce Height Decreased $h(n-1)\div h(n)$ |
|---|---|---|
| 0 | 233 | |
| 1 | 110 | 2.12 |
| 2 | 46.6 | 2.36 |
| 3 | 21 | 2.22 |
b. Model 4 is the best choice. The best choice for $a$ is $233$. $b = -0.8$ is a good choice as would any value based on two of the points given in the table or the value you would get by averaging the quotients in column 3 of the table from part (a).
c. The bounce height will be greater than 1 inch on the 6th bounce and less than 1 inch on the 7th bounce.
d. The best characterization is the third statement, "Mika is correct that the model predicts that the bounces will all be less than a thousandth of an inch, but in reality the ball will be at rest before it has bounced 50 times."
This is a 3 point task.
2 points for choosing Model 4 and having reasonable values for $a$ and $b$, knowing that the 7th bounce is the first that is less than an inch, but not identifying the correct characterization of Mika's claim.
2 points for choosing Model 4 and having reasonable values for $a$ and $b$ and identifying the correct characterization of Mika's claim but missing the 7th bounce.
1 point for choosing the incorrect model but correctly applying the model to find the first bounce that is less than an inch and identifying the correct characterization of Mika's claim.
Basketball Bounces, Assessment Variation 1
SCREEN I
In science class, some students dropped a basketball and allowed it to bounce. They measured and recorded the highest point of each bounce.
The students’ data is shown in the table and scatterplot. The first data point ($n = 0$) represents the height of the ball the moment the students dropped it.
|
Bounce Number $n$ |
Measured Height in Inches $h(n)$ |
|---|---|
| 0 | 233 |
| 1 | 110 |
| 2 | 46.6 |
| 3 | 21 |

In this task, you will choose a function to model the data and use the model to answer some questions.
SCREEN II
a. Compute the first three values in the last column of the table below.
|
Bounce Number $n$ |
Measured Height in Inches $h(n)$ |
Factor by which Bounce Height Decreased $h(n-1)\div h(n)$ |
|---|---|---|
| 0 | 233 | |
| 1 | 110 | [____________] |
| 2 | 46.6 | [____________] |
| 3 | 21 | [____________] |
[Student could choose to open up a scientific calculator.]
SCREEN III
b. Let $n$ be the bounce number and $h(n)$ be the height. Consider the following general forms for different kinds of models where $a$ and $b$ represent numbers:
| Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|
| $h(n) = a\cdot n+b$ | $h(n) = a\cdot n^2+b$ | $h(n) = \frac{a}{n} +b$ | $h(n) = a\cdot e^{bn}$ |
Which of the models shown is most appropriate to use for the given data?
Given the data above, what are reasonable values for $a$ and $b$ if we want to create a specific model to fit the data? Write the appropriate values in the equation below.
[Based on the choice students make above, they are given the appropriate template below. Here is the template for the exponential model]

c. Based on your model, what will be the first bounce with a maximum height that is less than 1 inch?
[When the student clicks "Next" from this screen, they get a message, "Are you sure you are ready to go on? You cannot change any of your previous answers after you continue from this screen."]
SCREEN IV
d. Mika said,
The model I came up with is $h(n) = 233 \cdot e^{-0.8n}$. I used it to predict that after 50 bounces, the height of the bounces will be less than a thousandth of an inch. It is good to have the model because it would be very difficult to measure such small heights.
What is the best way to characterize Mika's claim?
- Mika's claim is true. The whole point of using models is to make predictions.
- Mika's claim is true but she should give a more precise bound for the height of the ball after 50 bounces because the heights will be much much smaller than one thousandth of an inch.
- Mika is correct that the model predicts that the bounces will all be less than a thousandth of an inch, but in reality the ball will be at rest before it has bounced 50 times.
- Mika is not using the model appropriately. Models can't be used to make predictions past the given data, only between data points.
- Mika is not using the model appropriately. The model doesn't fit the data very well so it can't be used to make predictions that far in the future.
- Mika's claim is not true. The model states that the ball will be at rest before it gets to 50 bounces so the bounce heights will be zero, which is easy to measure.
