Block Scheduling
Task
A random sample of 100 students from a specific high school resulted in 45% of them favoring a plan to implement block scheduling. Is it plausible that a majority of the students in the school actually favor the block schedule? Simulation can help answer the questions.
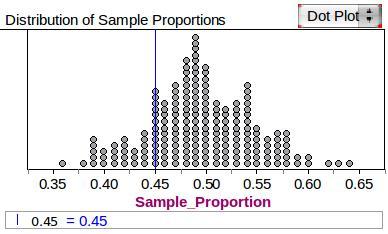
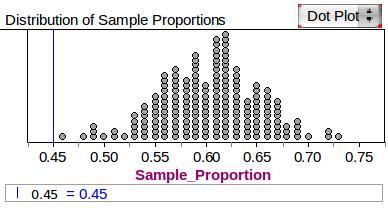
The accompanying plot shows a simulated distribution of sample proportions for samples of size 100 from a population in which 50% of the students favor the plan, and another distribution from a population in which 60% of the students favor the plan. (Each simulation contains 200 runs.)
- What do you conclude about the plausibility of a population proportion of 0.50 when the sample proportion is only 0.45?
- What about the plausibility of 0.60 for the population proportion?
IM Commentary
Students should understand the nature of statistical reasoning under uncertainty, as exemplified here, and the role of simulation in producing data that allows them to arrive at such conclusions. If an observed result can be reproduced as happening quite frequently under an assumed model, the model cannot be denied as plausible. If an observed result can be reproduced only rarely, or not at all, under an assumed model, the model can be denied plausibility. Statistical analyses do not provide proofs; they provide ways of weighing evidence.
In this task, output is given from a computer-generated simulation, generating size-100 samples of data from an assumed school population of 2000 students under hypotheses about the true distribution of yes/no voters. The task could be elongated (and accentuated) by having students operate a statistical software program to generated their data themselves, in which case the school population becomes a relevant (and unprovided) piece of information. The discussion of the significance of this number also contributes adherence to the S-IC standards -- for example, students might consider the significance of the data provided if the high school had 100, or even 105, students.
Solution
- When sampling 100 students from a population in which 50% of the students favor the plan, the data indicate that a sample proportion of 45% (or less) is quite likely to occur. Thus, a population proportion of 0.50 is plausible, given the observed sample result.
- When sampling 100 students from a population in which 60% of the students favor the plan, the data indicate that a sample proportion of 45% (or less) is quite unlikely. Thus, a population proportion of 0.60 is not plausible, given the observed sample result.
Block Scheduling
A random sample of 100 students from a specific high school resulted in 45% of them favoring a plan to implement block scheduling. Is it plausible that a majority of the students in the school actually favor the block schedule? Simulation can help answer the questions.
The accompanying plot shows a simulated distribution of sample proportions for samples of size 100 from a population in which 50% of the students favor the plan, and another distribution from a population in which 60% of the students favor the plan. (Each simulation contains 200 runs.)
- What do you conclude about the plausibility of a population proportion of 0.50 when the sample proportion is only 0.45?
- What about the plausibility of 0.60 for the population proportion?


