Do You Fit In This Car?
Task
Automobile manufacturers have to design the driver’s seat area so that both tall and short adults can sit comfortably, reach all the controls and pedals, and see through the windshield. Suppose a new car is designed so that these conditions are met for people from 58 inches to 76 inches tall.
The heights of adult men in the United States are approximately normally distributed with a mean of 70 inches and a standard deviation of 3 inches. Heights of adult women are approximately normally distributed with a mean of 64.5 inches and a standard deviation of 2.5 inches. What percentage of men in the United States is this car not designed to accommodate? What percentage of women in the United States is this car not designed to accommodate?
IM Commentary
This task requires students to use the normal distribution as a model for a data distribution. Students must use given means and standard deviations to approximate population percentages.
There are several ways (tables, graphing calculators, or statistical software) that students might calculate the required normal percentages. Depending on the method used, answers might vary somewhat from those shown in the solution.
In problems involving the normal distribution, encourage students to sketch the appropriate normal distribution and to shade the area that corresponds to the desired probability before using tables or technology to obtain the probability.
Solution
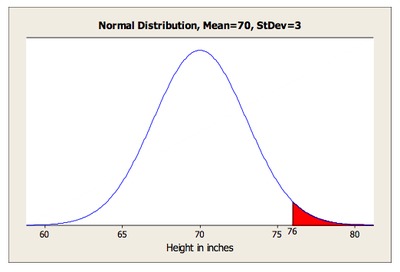
For men, we want the percentage of the normal distribution with mean 70 and standard deviation 3 that is above 76 inches or below 58 inches. Since 58 is 4 standard deviations below 70, the percentage below 58 is insignificant, so all we need is the percentage above 76, which corresponds to the shaded region in the diagram below. The area of this region is 0.0228, so about 2.3% of adult men won’t fit in this car.
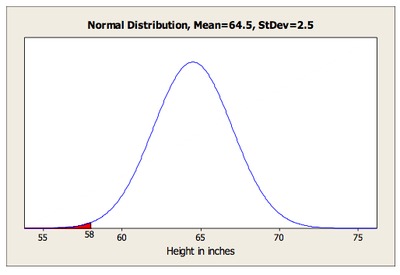
For women, 76 inches is $\frac{76-64.5}{2.5}=4.6$ standard deviations above the mean, so essentially 0% of women are too tall for the car. Thus, all we need is the percentage below 58 inches, which corresponds to the shaded region in the diagram below. The area of this region is 0.00466, so about 0.5% of adult women won’t fit in this car.
Do You Fit In This Car?
Automobile manufacturers have to design the driver’s seat area so that both tall and short adults can sit comfortably, reach all the controls and pedals, and see through the windshield. Suppose a new car is designed so that these conditions are met for people from 58 inches to 76 inches tall.
The heights of adult men in the United States are approximately normally distributed with a mean of 70 inches and a standard deviation of 3 inches. Heights of adult women are approximately normally distributed with a mean of 64.5 inches and a standard deviation of 2.5 inches. What percentage of men in the United States is this car not designed to accommodate? What percentage of women in the United States is this car not designed to accommodate?
