Laptop Battery Charge
Task
Jerry forgot to plug in his laptop before he went to bed. He wants to take the laptop to his friend's house with a full battery. The pictures below show screenshots of the battery charge indicator after he plugs in the computer at 9:11 a.m.

- The screenshots suggest an association between two variables. What are the two variables in this situation?
- Make a scatter plot of the data.
- Draw a line that fits the data and find the equation of the line.
- When can Jerry expect to have a fully charged battery?
IM Commentary
This task uses a situation that is familiar to students to solve a problem they probably have all encountered before: How long will it take until an electronic device has a fully charged battery? The goal of the task is to find and use a linear model answer this question.
One of the hardest problems for students in using quantitative reasoning is the clear definition of the quantities involved in a problem. Part (a) sounds very simple, but it is often harder than we think for students. Once we have a clear understanding of the variables we are investigating, the rest of the problem follows the usual procedure: Make a scatter plot, fit a line, use the line to answer the question.
In 8th grade students informally fit a line. This means that they can eyeball a line that approximates the relationship between the variables. A good tool to do this is an uncooked spaghetti or other thin stick that can be moved around. If computers are available, a program like GeoGebra or Desmos could also be used to make the scatter plot and to draw and manipulate (by "hand") a line that fits the data. Students will often try to find a line that hits as many data points as possible rather than find a line that may not hit many (or any) points exactly but is a good fit on average. This can lead to a productive class room discussion about the pros and cons of different lines and ultimately to why the linear regression line is a good approximation method. In high school, students will use technology to find the "best fit" least squares regression line.
This task can be used for instruction or assessment. If done in class, a discussion could include if a line is the best model for this situation. Close inspection shows that there seems to be some downward curvature to the data, which may agree with students' experiences when waiting for batteries to charge.
The task provides good opportunities for students to engage in SMP 2 - Reason Abstractly and Quantitatively as well as SMP 4 - Model with Mathematics.
Solution
- The two variables are time, $t$ and battery charge, $b$. There are several ways we can choose the units. A reasonable choice is "time in minutes since the laptop was plugged in" and "battery charge in percentage of full, %"
-
The laptop started charging at 9:11 a.m. and it was initially 41% charged. If we let $t$ be time since the laptop was plugged in, this information corresponds to the point with coordinates $(0,41).$ Similarly, we can translate the information in the other screenshots into coordinate points: $(16, 56),\ (25, 64),\ (37, 74),\ (44, 79),\ (57, 86),\ (66, 91)$.

-
There are several different ways we can draw a line that "fits" the data. The goal is to find a line that does a reasonable job of approximating the pattern in the scatter plot. This means that it may not hit any points exactly, but it minimizes the distance between the line and the data points over all. There is a specific mathematical method that finds the line of best fit that students will see in grade 9. But for the purpose of this task, using an uncooked spaghetti or a ruler is appropriate.
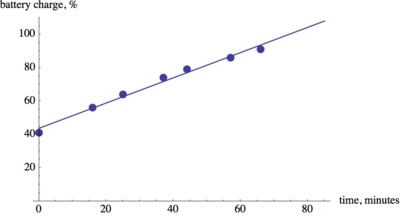
After drawing the line we can find its slope and read off the vertical intercept. For the line shown above (individual students may have different lines), it looks like the data point $(16,56)$ lies on the line and we can estimate a second point on the line, for example $(57,87)$. So the slope of the line is $\displaystyle{\frac{(87-56)}{(57-16)}=\frac{31}{41}\approx0.76}$. The vertical intercept is close to 43. Therefore, the equation of the line is $b=0.76t+43.$
Note that we estimated the coordinates of the points on the line that we used to find the equation. Depending on how carefully the line is drawn and the coordinates are estimated, the equations students come up with may differ.
It is also worth noting that the vertical intercept of the line is slightly higher than the actual battery charge when the computer was plugged in. This also illustrates that the line is a good approximation of the battery charge on average but does not agree with the exact data we collected.
-
We can extend the line of best fit and see at what time it will reach an output value of 100%. This happens about 75 minutes after the computer was plugged in.
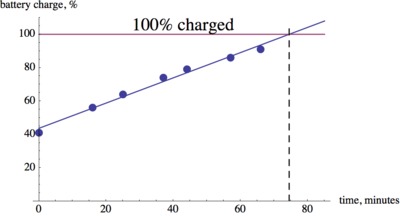
We can also use the equation to solve $0.76t+43=100$ for $t$ to obtain $t= 75$ minutes.
Laptop Battery Charge
Jerry forgot to plug in his laptop before he went to bed. He wants to take the laptop to his friend's house with a full battery. The pictures below show screenshots of the battery charge indicator after he plugs in the computer at 9:11 a.m.

- The screenshots suggest an association between two variables. What are the two variables in this situation?
- Make a scatter plot of the data.
- Draw a line that fits the data and find the equation of the line.
- When can Jerry expect to have a fully charged battery?
