Are They Similar?
Task
Determine, using rotations, translations, reflections, and/or dilations, whether the two polygons below are similar.
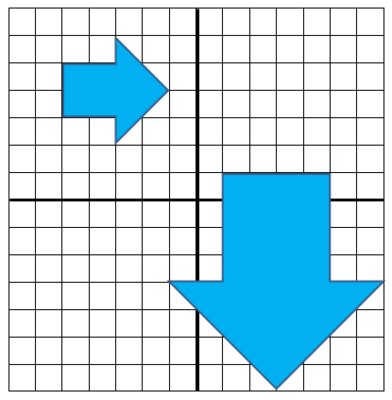
The intersection of the dark lines on the coordinate plane represents the origin (0,0) in the coordinate plane.
IM Commentary
This goal of this task is to provide experience applying transformations to show that two polygons are similar. If students have difficulty visualizing each transformation they may use tools such transparencies, scissors, or patty paper to help find their sequence of transformations. Since there are many ways to show a similarity students should be encouraged to share and examine each others' methods. The teacher may wish to point out that corresponding sides of these polygons are proportional, with a scale factor of 2, and corresponding angles are congruent: this relates the notion of similarity in terms of dilations and rigid motions to the notion of ''same shape, different size'' appropriate for younger students.
One natural extension of this task, focusing on communicating mathematical ideas and procedures clearly, involves letting students work in pairs. Student #2 can be given the image below, or a different image if the students have already worked on the arrows, to which she applies a sequence of transformations.
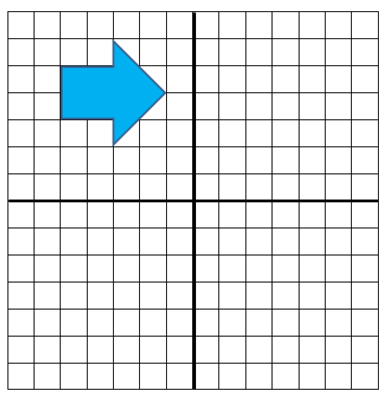
Student #1 then describes to Student #2 the sequence of transformations to apply to the polygon. They can then compare notes and come to agreement on what the transformed image should look like and where it should be.
Solutions
Solution:
There are many valid methods to transform the polygon and one of these is described here. This sequence has the advantage that it uses one translations, one rotation, one reflection, and one dilation. The first step is to reflect the polygon, labeled $ABCDEFG,$ over the $y$-axis:
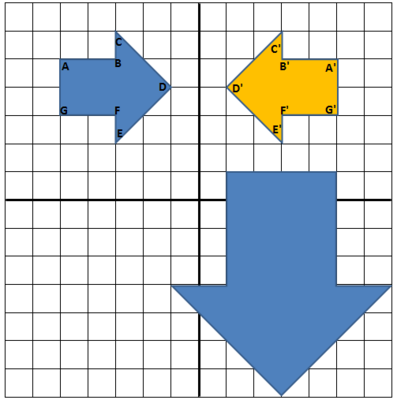
The image of $A$ has been denoted $A'$ and similarly for the other vertices of $ABCDEFG$. Reflection about the $y$-axis keeps the $y$-coordinate the same and multiplies the $x$-coordinate by $-1$. So, for example, $B = (-3,5)$ so $B' = (3,5)$.
Next we rotate $A'B'C'D'E'F'G'H'$ 90º counterclockwise about the point $(3, 4)$ (the center of the shape). This is pictured below, with the image of, for example, $A'$ being denoted as $A''$.
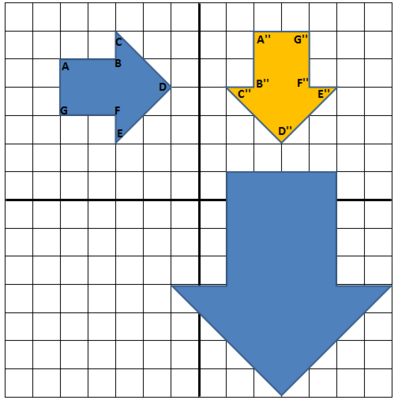
Next we translate $A''B''C''D''E''F''G''$ down 5 units and left 1 unit so that the image of point $A''$, denoted $A'''$, is the point $(1, 1)$. This is shown below:
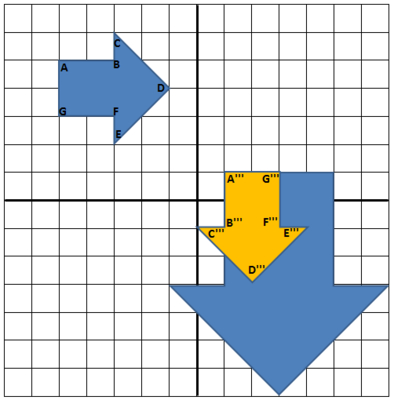
Lastly we dilate $A'''B'''C'''D'''E'''F'''G'''$ about $(1,1)$ with a scale factor of $2$. The center $A'''$ does not move when we apply this dilation. For the other vertices, we take $B'''$ as an example. The image of $B'''$ will be on $\overleftrightarrow{A'''B'''}$ but its distance from $A'''$ is twice that of $B'''$. Since $B'''$ lies on the vertical line $y=1$ and it is two units down from $(1,1)$, its image, $B''''$, will also lie on $y = 1$ but it will be $2 \times 2$ or $4$ units down from $(1,1)$. This means that $B'''' = (1,-3)$. All other vertices can be placed in a similar manner, with the result pictured below:
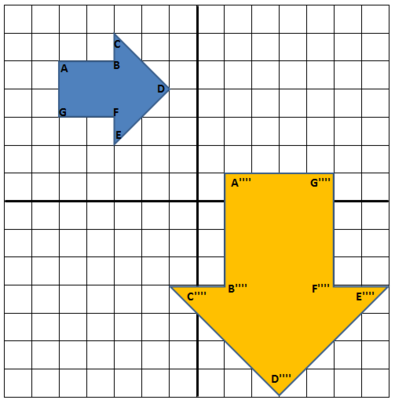
Notice that $A''''B''''C''''D''''E''''F''''G''''$ lies on top of the original (large) blue polygon and so we have shown that the two given polygons are similar.
Solution:
Are They Similar?
Determine, using rotations, translations, reflections, and/or dilations, whether the two polygons below are similar.

The intersection of the dark lines on the coordinate plane represents the origin (0,0) in the coordinate plane.
