Task
In this task, using computer software, you will apply reflections, rotations, and translations to a triangle. You will then study what happens to the side lengths and angle measures of the triangle after these transformations have been applied. In each part of the question, a sample picture of the triangle is supplied along with a line of reflection, angle of rotation, and segment of translation: the attached GeoGebra software will allow you to experiment with changing the location of the line of reflection, changing the measure of the angle of rotation, and changing the location and length of the segment of translation.
-
Below is a triangle $ABC$ and a line $\overleftrightarrow{DE}$:

Use the supplied GeoGebra application to reflect $\triangle ABC$ over $\overleftrightarrow{DE}$. Label the reflected triangle $A'B'C'$. What are the side lengths and angle measures of triangle $A'B'C'$? What happens when you change the location of one of the vertices of $\triangle ABC$? What happens when you change the location of line $\overleftrightarrow{DE}$?
-
Below is a triangle $ABC$ and a point $E$. Draw the rotation of $\triangle ABC$ about $E$ through an angle of 85 degrees in the counterclockwise direction.
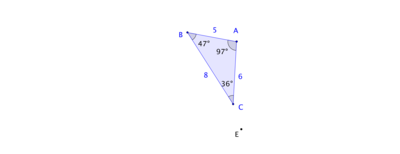
Label the image of $\triangle ABC$ as $\triangle A'B'C'$. What happens to the side lengths and angle measures of $\triangle A'B'C'$ when you change the measure of the angle of rotation? What happens when you move the center of rotation $E$?
-
Below is a triangle $ABC$ and a directed line segment $\overline{ED}$.

Draw the translation of $\triangle ABC$ by $\overline{ED}$ and label it $\triangle A'B'C'$. What happens to the side lengths and angle measures of triangle $A'B'C'$ when you change one of the vertices, $A$, $B$, or $C$? What if you change the position, length, or direction of the directed line segment $\overline{ED}$?
IM Commentary
The goal of this task is to use technology to visualize what happens to angles and side lengths of a polygon (a triangle in this case) after a reflection, rotation, or translation. GeoGebra files are attached below with triangles already constructed as shown in the images. Students familiar with this or other technology (such as Geometer's Sketchpad) can construct their own polygons as well as their own lines of reflection, angles and centers of rotation, and segments of translation. The supplied GeoGebra files keep track of side lengths and angle measures, allowing the students to gain visualization skills as they study how the transformed polygons vary.
The emphasis for this problem is on MP5, Use Appropriate Tools Strategically. Applying transformations accurately to geometric shapes is a challenging endeavor. Dynamic geometry software, however, does this part of the work, allowing students to focus on how the shapes and their images change when one or more pieces of information is altered. It is important for teachers to use the technology to good effect, having students change the line of reflection, center and angle of rotation, and directed segment of translation. In addition they can change the given triangle and observe how its reflected, rotated, or translated image varies.
Though this is not the focus of the task, the teacher may wish to highlight that in each part of the problem, $\triangle ABC$ is congruent to $\triangle A'B'C'$ in order to familiarize students with this important word and concept.
Solution
Each picture below shows the requested reflection, rotation, and translation applied to the given triangles.
-
No matter where you move the vertices of the polygon or the polygon itself, the reflected image will have the same corresponding side lengths and angle measures as the original polygon. Moving the line of reflection does not change this either.

-
No matter where you move the vertices of the polygon or the polygon itself, the rotated image will have the same corresponding side lengths and angle measures as the original polygon. Moving the center of rotation or changing the measure of the angle of rotation does not change this either.

-
No matter where you move the vertices of the polygon or the polygon itself, the translated image will have the same corresponding side lengths and angle measures as the original polygon. Moving the position, length, or direction of the directed line segment does not change this either.







