Chicken and Steak, Variation 1
Task
You have \$100 to spend on a barbeque where you want to serve chicken and steak. Chicken costs \$1.29 per pound and steak costs \$3.49 per pound.
-
Find a function that relates the amount of chicken and the amount of steak you can buy.
-
Graph the function. What is the meaning of each intercept in this context? What is the meaning of the slope in this context? Use this (and any other information represented by the equation or graph) to discuss what your options are for the amounts of chicken and amount of steak you can buy for the barbeque.
IM Commentary
This task presents a real world situation that can be modeled with a linear function best suited for an instructional context.
Part (a) is relatively straightforward, although the wording is left intentionally ambiguous about whether the amount of steak should be written as a function of the amount of chicken or the amount of chicken as a function of the amount of steak (both approaches are presented in the solutions shown below). Whenever we have a (non-constant) linear relationship between two quantities, we can always write either quantity as a function of the other, and students should understand that which variable is the dependent variable and which is the independent variable is a choice made by the modeler.
Part (b) is more open-ended. To fully explore part (b), students should interpret the horizontal and vertical intercepts of the graph, the slope of the graph, and the coordinates of points on the graph.
This task presents a good opportunity to have a discussion about choosing independent and dependent variables and interpreting slopes, intercepts, and generic points on the graph in the context. It is especially useful for students to see that, for example, the "steak-intercept" is interpreted in the same way regardless of whether the vertical or horizontal axis is the "steak-axis."
Solutions
Solution: steak as a function of chicken
Note that all numbers are rounded to two digits after the decimal. Therefore, all solutions are approximate.
-
Chicken costs \$1.29 per pound and steak costs \$3.49. We can spend a total of \$100. We don't know how many pounds of chicken and steak we are buying. So, let us assign variables to those two quantities. Let $$ c = \text{amount of chicken (in lbs)} $$ and $$ s = \text{amount of steak (in lbs)} $$
Then $1.29c$ gives us the total amount we pay for chicken, and $3.49s$ gives us the total amount we pay for steak. If we have only \$100 dollars to spend on chicken and steak together, we can write this relationship in the form of the equation $$ 1.29c + 3.49s = 100. $$ To find a function that relates the two variables, we can solve for one variable in terms of the other. Since the problem does not specify which of the two variables is the independent variable and which is the dependent variable, we can make a choice. Let $c$ be the independent variable; then we can find a equation that expresses $s$ in terms of $c$. In other words, we can find an equation of the form $s=f(c)$: \begin{align} 1.29c+3.49s &= 100\\ 3.49s &=100-1.29c \\ s=f(c) &= \frac{-1.29}{3.49}c +\frac{100}{3.49}\\ s=f(c) &= -0.37c+28.65 \end{align}
-
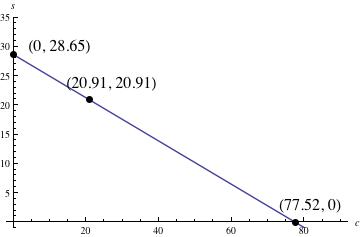
We can graph this function with $c$, the amount of chicken, on the horizontal axis and $s$, the amount of steak, on the vertical axis. The graph is a line with vertical intercept $(0, 28.65)$ and slope $-0.37.$ Since it does not make sense to talk about negative amounts of chicken or steak, we are only interested in the part of the line where both coordinates are non-negative, as shown below. We can find the horizontal intercept by setting the function equal to zero and solving for $c$: \begin{align} -0.37c+28.65&=0\\ 0.37c&=28.65\\ c&=77.52 \end{align} The graph shows all the options we have for chicken and steak combinations to buy for our barbeque. The vertical intercept shows that we can buy at most 28.65 pounds of steak if we choose not to buy any chicken at all. On the other extreme, the horizontal intercept shows that we can buy 77.52 pounds of chicken if we don't buy any steak. If we want equal amounts of chicken and steak, we can let $s=c$ in our function and solve for $c$: \begin{align} -0.37c+28.65&=c\\ 1.37c&=28.65\\ c&=20.91 \end{align} This means that we can buy 20.91 pounds of chicken and 20.91 pounds of steak for 100 dollars. The slope of the line is -0.37. This means that for every additional pound of chicken we want to buy, we have to decrease the amount of steak by 0.37 pounds.
Solution: chicken as a function of steak
Note that all numbers are rounded to two digits after the decimal. Therefore, all solutions are approximate.
-
We can start again by writing the equation relating the amounts of chicken and steak we can buy for \$100 dollars: $$ 1.29c + 3.49s = 100. $$ This time we let $s$ be the independent variable and $c$ the dependent variable. Then we can find an equation $c=g(s)$ that represents $c$ as a function of $s$: \begin{align} 1.29c+3.49s &= 100\\ 1.29c &=100-3.49s \\ c=g(s) &= \frac{-3.49}{1.29}s +\frac{100}{1.29}\\ c=g(s) &= -2.71s+77.52 \end{align}
-
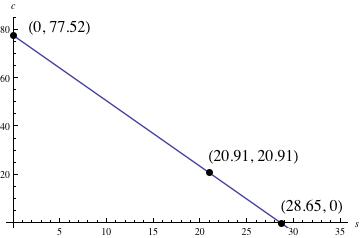
We can graph this function with $s$, the amount of steak, on the horizontal axis and $c$, the amount of chicken, on the vertical axis. The graph is a line with vertical intercept $(0, 77.52)$ and slope $-2.71.$ Since it does not make sense to talk about negative amounts of chicken or steak, we are only interested in the part of the line where both coordinates are non-negative, as shown below. We can find the horizontal intercept by setting the function equal to zero and solving for $s$. This gives $s=28.65$.
The graph shows all the options we have for chicken and steak combinations to buy for our barbeque. The vertical intercept shows that we can buy at most 77.52 pounds of chicken if we choose not to buy any steak at all. On the other extreme, the horizontal intercept shows that we can buy 28.65 pounds of steak if we don't buy any chicken. If we want equal amounts of chicken and steak, we let $c=s$ and solve fore $s$. Just as before we find that we can buy 20.91 pounds of chicken and 20.91 pounds of steak for 100 dollars.
The slope of the line is -2.71. This means that for every additional pound of steak we want to buy, we have to decrease the amount of chicken by 2.71 pounds.
Chicken and Steak, Variation 1
You have \$100 to spend on a barbeque where you want to serve chicken and steak. Chicken costs \$1.29 per pound and steak costs \$3.49 per pound.
-
Find a function that relates the amount of chicken and the amount of steak you can buy.
-
Graph the function. What is the meaning of each intercept in this context? What is the meaning of the slope in this context? Use this (and any other information represented by the equation or graph) to discuss what your options are for the amounts of chicken and amount of steak you can buy for the barbeque.
