Ratio of boys to girls
Task
The ratio of the number of boys to the number of girls at school is 4:5.
What fraction of the students are boys?
- If there are 120 boys, how many students are there altogether?
IM Commentary
In some textbooks, a distinction is made between a ratio, which is assumed to have a common unit for both quantities, and a rate, which is defined to be a quotient of two quantities with different units (e.g. a ratio of the number of miles to the number of hours). No such distinction is made in the common core and hence, the two quantities in a ratio may or may not have a common unit. However, when there is a common unit, as in this problem, it is possible to add the two quantities and then find the ratio of each quantity with respect to the whole (often described as a part-whole relationship).
Tasks like these help build appropriate connections between ratios and fractions. Students often write ratios as fractions, but in fact we reserve fractions to represent numbers or quantities rather than relationships between quantities. For example, if we were to consider the ratio $4:5$ in this situation, then two possible ways to interpret $\frac45$ in the context are to say,
"The number of boys is $\frac45$ the number of girls,"
or to say,
"The ratio of the number of boys to the number of girls is $\frac45 : 1$."
This second interpretation reflects the fact that $\frac45$ is the unit rate (which is a number) for the ratio $4:5$.
Solutions
Solution: Using a tape diagram
For every 4 boys there are 5 girls and 9 students at the school. So that means that $\frac49$ of the students are boys. $\frac49$ of the total number of students is 120 students: $$\frac49 \times ? = 120$$ If $\frac49$ the number of students is 120, then $\frac14$ of 120 is $\frac19$ of the total number of students. In other words, $\frac14 \times 120 = 30$ is $\frac19$ the total number of students. Then 9 times this amount will give the total number of students: $$9\times 30 = 270$$ So there is a total of 270 students at the school. Note that this is equivalent to finding the answer to the division problem: $$120\div \frac49 =?$$ We can see all of this very succinctly by using a tape diagram:
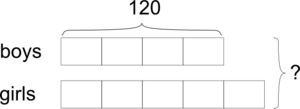
-
There are 4 units of boys and 9 units of students. Therefore 4/9 of the students are boys.
-
4 units = 120
1 unit = 30
9 units = 270
There are 270 students altogether.
Solution: Using a table
| Boys | Girls | All students |
| 4 | 5 | 9 |
| 40 | 50 | 90 |
| 80 | 100 | 180 |
| 120 | 150 | 270 |
Students can multiply the numbers in the first row by 10 to get the second row, and then double that amount to get the third row. Adding the entries in the second and third row gives the fourth row that has the solution.
Alternatively, since $120 \div 4 = 30$, students can just multiply the numbers in the first row by 30 to get the values in the fourth row.
- In every row, we can see that the fraction of the students that are boys is $\frac{4}{9} $.
- looking at the last row, we can see that the total number of students will be $4\times 30 + 5 \times 30 = 120 + 150 = 270$.
Ratio of boys to girls
The ratio of the number of boys to the number of girls at school is 4:5.
What fraction of the students are boys?
- If there are 120 boys, how many students are there altogether?
