Making Hot Cocoa, Variation 2
Task
A recipe for hot chocolate calls for 3 cups of milk. What fraction of the recipe can Nelli make with $\frac23$ cups of milk?
-
Solve the problem by drawing a picture.
-
Explain how you can see the answer to the problem in your picture.
-
Which of the following multiplication or divisions equations represents this situation? Explain your reasoning. $$3\times\frac23=? \qquad 3\div\frac23=? \qquad \frac23\div3=?$$
Solve the arithmetic problem you chose in part (c) and verify that you get the same answer as you did with your picture.
IM Commentary
This is the second of two fraction division tasks that use similar contexts to highlight the difference between the “Number of Groups Unknown” a.k.a. “How many groups?” when the quotient is a fraction (or mixed number) greater than 1 (Variation 1) and when the quotient is a fraction that is less than 1 (Variation 2). Even when students understand this type of division context when they involve whole numbers, the transition to division problems involving fractions is not easy. In order to successfully make this transition, students must have a solid understanding of multiplication and division with whole numbers and multiplication with fractions.
These two tasks are meant as instructional tasks, with the idea that students who can solve these problems with diagrams may or may not see the connection to division. Thus, the tasks ask students to make this connection explicit.
There are significant language issues when moving from whole number to fraction division when the quotient is less than 1. In that case, it might help to point out that “Number of Groups Unknown” is better characterized as “Fraction of a Group Unknown” a.k.a. “What fraction of a group?” and the alternate of “Group Size Unknown” would be worded “How much in each group?”
Solution
-
Below is a picture that can be used to solve the problem.
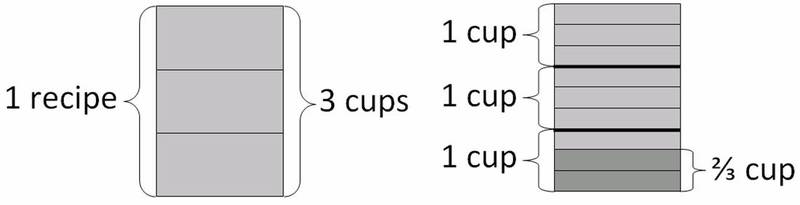
-
From the given information we know that one recipe calls for 3 cups of milk. The question is really asking, “What fraction of a recipe can be made with $\frac23$ cups of milk?” First we break the recipe into 3 rectangles, each representing one cup. We then break each of those cups into 3 rectangles, each representing one-third of a cup. We shade 2 of smallest rectangles, which represent the $\frac23$ cups of milk we have. Now we can see that the $\frac23$ cups of milk is actually $\frac29$ of a recipe because two rectangles are shaded, while nine rectangles make up the whole recipe.
-
Again, we are trying to answer the question, “What fraction of a recipe can be made with $\frac23$ cups of milk?” This is really a ‘How many groups’ or ‘What fraction of a group’ question. Hence it is a division problem. We are trying to find how many groups of 3 cups are in $\frac23$ cups, so the correct equation is:
$$\frac23\div3=?$$ -
Solve the arithmetic problem you chose in part (c) and verify that you get the same answer as you did with your picture.
$$ \begin{align} \frac23\div3&= \\ &=\frac23\div\frac31 \\ &=\frac23\times\frac13\\ &= \frac29 \end{align} $$By comparing the picture with part (c), we see that our answers are the same.
Making Hot Cocoa, Variation 2
A recipe for hot chocolate calls for 3 cups of milk. What fraction of the recipe can Nelli make with $\frac23$ cups of milk?
-
Solve the problem by drawing a picture.
-
Explain how you can see the answer to the problem in your picture.
-
Which of the following multiplication or divisions equations represents this situation? Explain your reasoning. $$3\times\frac23=? \qquad 3\div\frac23=? \qquad \frac23\div3=?$$
Solve the arithmetic problem you chose in part (c) and verify that you get the same answer as you did with your picture.
