Base and Height
Task
Mrs. Lito asked her students to label a base $b$ and its corresponding height $h$ in the triangle shown.

Three students drew the figures below.
-
Raul

-
Mark

-
Kiki

- Which students, if any, have correctly identified a base and its corresponding height? Which ones have not? Explain what is incorrect.
- There are three possible base-height pairs for this triangle. Sketch all three.
IM Commentary
It is common for students to think that the base of a triangle must be the side that is on the "bottom" of the triangle. So students might be tempted to say that Raul has not correctly identified a base and height for the triangle. The mistakes that Mark and Kiki have made also represent common errors. The purpose of this task is to help students understand what is meant by a base and its corresponding height in a triangle and to be able to correctly identify all three base-height pairs.
Teachers might use this task to explicitly guide students in attending to precision (Standard for Mathematical Practice 6) by, for example, adding the following instructions:
For each sketch,
-
Your explanation should use precise vocabulary including, for example,
- perpendicular
- vertex
- base
- height
- segment
- corresponding height
- sides
- angle
- adjacent
- 90 degrees.
Your sketches should correctly identify the three base-height pairs for Mrs. Lito's triangle.
Solution
-
Raul (A.) is the only student that has correctly identified a base and its corresponding height. Raul’s base and height are correct because his height, $h$, is the length of the perpendicular segment from the line determined by his base to the vertex of the triangle opposite the base.
Mark (B.) and Kiki (C.) have not correctly identified a base and corresponding height.
Mark drew his figure like this:

The segment that Mark labeled $h$ is actually just one of the sides of the triangle that is adjacent to the base that he labeled. The picture does not tell us that the angle between the segments that Mark labeled $b$ and $h$ is 90 degrees. This means that we cannot assume that the adjacent side is perpendicular to the base. If we use the same base that Mark used, then the corresponding height should look like this:

The length of the blue line is the correct height for the base that Mark chose because this segment is perpendicular to Mark’s base.
Kiki drew her figure like this:

The segment that Kiki labeled $b$ is not one of the sides of the triangle. The base of a triangle must be one of the sides of the triangle. The base that goes with the height that Kiki drew looks like this:
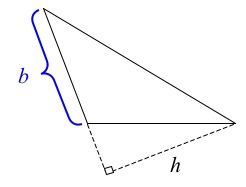
The blue base is the correct base for the height that Kiki drew. This segment is one of the sides of the triangle and, because of this, can be chosen as a base. The height that Kiki drew is the length of the perpendicular segment from the line determined by this base to the vertex of the triangle that is opposite the base.
-
As mentioned above, the three correct base-height pairs are:



Base and Height
Mrs. Lito asked her students to label a base $b$ and its corresponding height $h$ in the triangle shown.

Three students drew the figures below.
-
Raul

-
Mark

-
Kiki

- Which students, if any, have correctly identified a base and its corresponding height? Which ones have not? Explain what is incorrect.
- There are three possible base-height pairs for this triangle. Sketch all three.
