-
If Shauna buys a 3 foot long sandwich and cuts it into pieces that are $\frac12$ foot long, her sandwich would look something like the picture below.

By looking at the picture above, we can see that there are 6 pieces that are $\frac12$ foot long, which gives the same answer as if we were to compute $3 \div \frac12$.
We can also think about this problem without the help of a picture. Shauna has a sandwich that is 3 feet long. If she slices that sandwich into pieces so that each piece is $\frac12$ foot long and wants to know how many sandwich slices she would get, Shauna is really asking, “How many groups of $\frac12$ are in 3?” which is one of the interpretations of $3 \div \frac12$.
-
If Phil makes 3 quarts of soup for dinner, and his family eats half of the soup for dinner, his situation would look something like the picture below.
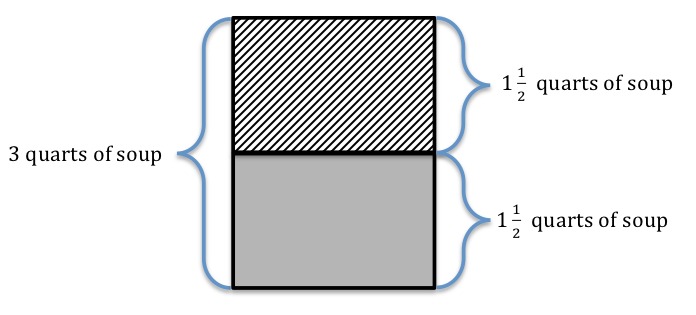
From this picture above, we can see that Phil’s family ate $1 \frac12$ quarts of soup. This problem cannot be modeled by $3\div \frac12$.
We can also think about this problem without the help of a picture. If Phil makes 3 quarts of soup for dinner, and his family eats $\frac12$ of the soup he made, then his family really ate $\frac12$ of the 3 quarts of soup. This is the meaning of $\frac12 \times 3=\frac12 \times \frac31= \frac32=1 \frac12$, not $3 \div \frac12=6$.
-
If a pirate finds 3 pounds of gold and hides an equal amount of gold in each of 2 chests, his situation would look something like the picture below.

From the picture above, we can see that each chest would hold half of the three pounds of gold, or $1 \frac12$ pounds of gold. This problem cannot be modeled by 3÷1/2.
We can also think about this problem without the help of a picture. If a pirate finds 3 pounds of gold, hides an equal amount of gold in each chest, and wants to know how much gold is in each chest, he is really asking, “How much is in each group if 3 is evenly distributed amongst 2 groups?” This is the meaning of $3 \div 2 = 3 \div \frac21= \frac31 \times \frac12= \frac32=1 \frac12$, not $3 \div \frac12=6$.
-
 From the picture above, we can see that if 3 cups of flour is $\frac12$ the bag, then 6 cups of flour were in the bag to start.
From the picture above, we can see that if 3 cups of flour is $\frac12$ the bag, then 6 cups of flour were in the bag to start.
This problem is asking "3 cups is $\frac12$ of what amount?" which we can represent symbolically like this:
$$\frac12 \times ? = 3$$
which is equivalent to
$$3\div \frac12 = 6$$
This is the "How many in one group?" interpretation of $3\div \frac12$.




 From the picture above, we can see that if 3 cups of flour is $\frac12$ the bag, then 6 cups of flour were in the bag to start.
From the picture above, we can see that if 3 cups of flour is $\frac12$ the bag, then 6 cups of flour were in the bag to start.