Writing a Mixed Number as an Equivalent Fraction
Task
Ben wrote a mixed number as the fraction 7$\frac{1}{3}$. Here is his work:
Explain what Ben did in each step.
IM Commentary
This task relates to one aspect of 4.NF3.c, namely writing a mixed number as an equivalent fraction; other tasks illustrate other aspects of this standard. The purpose of this task is to help students understand and articulate the reasons for the steps in the usual algorithm for converting a mixed number into an equivalent fraction, that is
$$A\frac{B}{C} = \frac{(A\times C)+B}{C}$$
Step two shows that the algorithm is merely a shortcut for finding a common denominator between two fractions. This concept is an important precursor to adding mixed numbers and fractions with like denominators and as such, step two should be a point of emphasis.
This task is appropriate for either instruction or formative assessment, and dovetails nicely with MP 3, Construct viable arguments and critique the reasoning of others. If the goal is to get students to explain the steps using pictures, then more guidance might be necessary.
A natural extension or complement to this task would be to perform and justify the reverse of these steps, that is, going from a fraction greater than 1 to a mixed number.
Solutions
Solution: Soultion 1
Recall that 7$\frac{1}{3}$ is shorthand for $7+\frac{1}{3}$, and that $7=\frac{7}{1}$.
So in Step 1, Ben is writing $7\frac{1}{3}$ as $7+\frac{1}{3}$ and then writing 7 as $\frac{7}{1}$.
In Step 2, Ben found an equivalent fraction for $\frac{7}{1}$ so that it would have the same denominator as $\frac{1}{3}$:
$$\frac{7}{1}+\frac{1}{3} = \frac{(7\times 3)}{(1\times 3)}+\frac{1}{3} = \frac{(7\times 3)}{3}+\frac{1}{3}$$
and then he added them together
$$\frac{(7\times 3)}{3}+\frac{1}{3}= \frac{(7\times 3)+1}{3}$$
In Step 3, Ben found the product $(7\times 3)=21$.
In Step 4, he added 21 and 1 in the numerator.
Solution: Solution 2
Ben's solution can be also represented by the shaded portion of the pictures below:
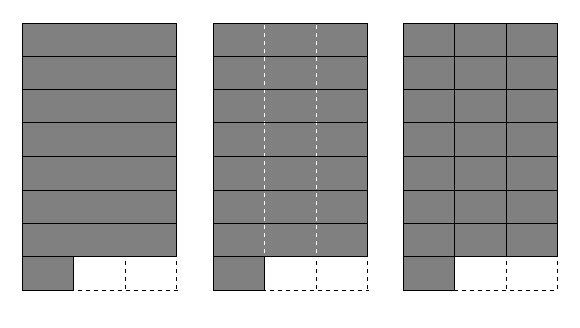
In the first picture we have 7 wholes together with $\frac{1}{3}$ of a whole. This represents $7\frac{1}{3}$ but can also be interpreted as $\frac{7}{1}+\frac{1}{3}$ and so illustrates what Ben wrote in Step 1.
In the next picture, each of the 7 wholes is divided into three equal parts, giving us $(7\times 3)$ thirds together with 1 extra third. This illustrates Step 2 of Ben's work: $$7\frac{1}{3}= \frac{(7\times 3)+1}{3}$$
Finally, in the third picture we can count up all the thirds and see we have 21 from the 7 wholes and 1 more, for a total of 22 thirds. So our final answer is $\frac{22}{3}$. By interpreting the pictures appropriately, we can make sense of Ben's Step 3 and Step 4.
Writing a Mixed Number as an Equivalent Fraction
Ben wrote a mixed number as the fraction 7$\frac{1}{3}$. Here is his work:
Explain what Ben did in each step.
