Addition Patterns
Task
Below is a table showing addition of numbers from $1$ through $5$.
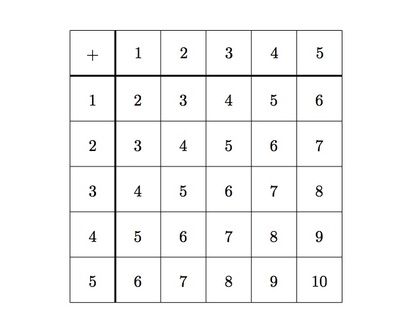
-
In each column and each row of the table, even and
odd numbers alternate. Explain why.
-
Explain why the diagonal, from top left to bottom right, contains the even
numbers $2,4,6,8,$ and $10$.
-
Explain why all numbers in the other diagonal, from bottom left to top right,
are $6$'s.
IM Commentary
The purpose of this task is to study some patterns in a small addition table. Each pattern identified persists for a larger table and if more time is available for this activity students should be encouraged to explore these patterns in larger tables. This task is intended for instructional purposes. The goal is to study the structure of the table and relate this to properties of addition.
The "checkerboard pattern'' of even and odd numbers comes from the fact that adding one to an even (respectively odd) number produces an odd (respectively even) number. The first five even numbers appearing on the diagonal comes from the fact that an even number $2n$ can be written as $n + n$: in this case, this is shown for $n = 1,2,3,4,5$. The fact that the other diagonal has all $6$'s comes from the fact that moving up one in the table means that one addend decreases by one while moving to the right one in the table means that the other addend increases by one: the increase and decrease cancel out so the sum remains the same on these diagonals.
Solution
-
The alternating odd and even numbers in the rows and columns is captured in the following picture:

The reason for the alternating pattern is that each time we move to the right one box or down one box, we are adding one more to our sum. For example,
$$\begin{align} (2+3) +1 &= 2 + (3 +1)\\ &= 2+4 \end{align}$$shows what happens when you move one box to the right from the entry for $2+3$ (note that this is an example of the associative property of addition). An even number plus one gives an odd number:
while an odd number plus one gives an even number:

so this explains the alternating pattern.
-
The diagonal with the first five even whole numbers is colored in blue below:

The reason why these numbers are even is that the first blue box comes from finding the sum $1 + 1$, the second blue box comes from finding the sum $2 + 2$, and so on. If we double the numbers in the sequence 1, 2, 3, 4, 5 we get the sequence 2, 4, 6, 8, 10.
-
The numbers on the diagonal going from bottom left to top right are shaded blue in the following picture:

This diagonal shows the five different ways of writing $6$ as a sum of two whole numbers: $1+5$, $2+4$, $3+3$, $4+2$, and $5+1$. Each time we move up one the first summand is decreased by one while each move to the right increases the second summand by one. What we are using, in effect, is the associative property of addition. For example:
$$\begin{align} 1+5 &= 1 + (1 +4 )\\ &= (1+ 1) + 4\\ &= 2+4 \end{align}$$The net effect is to obtain the same total of $6$ when adding.
Addition Patterns
Below is a table showing addition of numbers from $1$ through $5$.

-
In each column and each row of the table, even and
odd numbers alternate. Explain why.
-
Explain why the diagonal, from top left to bottom right, contains the even
numbers $2,4,6,8,$ and $10$.
-
Explain why all numbers in the other diagonal, from bottom left to top right,
are $6$'s.
