Toll Bridge Puzzle
Task
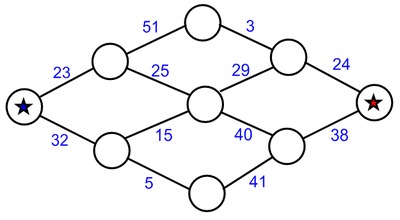
The picture shows islands connected by bridges. To cross a bridge, you must pay a toll in coins. If you start on the island marked in blue with 100 coins, how can you make it to the island marked in red?
IM Commentary
This task is intended to assess adding of four numbers as given in the standard while still being placed in a problem-solving context.
As written this task is instructional; due to the random aspect regarding when the correct route is found, it is not appropriate for assessment.
This puzzle works well as a physical re-enactment, with paper plates marking the islands and strings with papers attached for the tolls.
Students will often be tempted by the single digit numbers to assume the route has to pass that way. They may also miss the "crossover" using the central island, finding the 23 + 25 + 29 + 24 route and the 32 + 15 + 40 + 38 route but not the 23 + 25 + 40 + 38 route or the 32 + 15 + 29 + 24 one.
Technically, paths that run from right to left along some bridges could be considered as well (for example, 32 + 5 + 41 + 40 + 29 + 24). However, for this particular example, such paths can be ignored since students will find a cheap enough path by only investigating paths that run from left to right. One might be tempted to modify the problem by having the student start with 99 coins, and ask if it is possible to reach the red island. However, such a modification would be inappropriate since a mathematically valid solution would require that the student consider all paths, including those that cross some bridges from right to left.
Solution
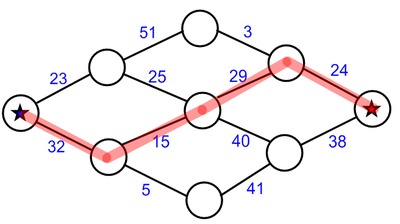
32 + 15 + 29 + 24 = 100
Other possible routes:
23 + 51 + 3 + 24 = 101
23 + 25 + 29 + 24 = 101
23 + 25 + 40 + 38 = 126
32 + 15 + 40 + 38 = 116
32 + 5 + 41 + 38 = 116
Toll Bridge Puzzle
The picture shows islands connected by bridges. To cross a bridge, you must pay a toll in coins. If you start on the island marked in blue with 100 coins, how can you make it to the island marked in red?

